Ez a cikk azoknak készült akik szeretnének szemléletes képet kapni arról, hogy mi az a konvolúció, vagy például honnan jön a konvolúció képlete.
A konvolúció lényegében az átlag fogalmának az általánosítása. Itt csak az egydimenziós konvolúcióról fogok írni, de ha ezt megértettük, akkor már magasabb dimenzióra is könnyebb elképzelni.
Ahhoz, hogy megértsük a konvolúció fogalmát, először a diszkrét változattal érdemes kezdeni. Ehhez lássuk először a tőzsdét! Furcsa lehet, hogy a tőzsdével kezdjük,és elsőre távolinak tűnhet a példa, de a diszkrét konvolúció szemléltetéséhez ez az egyik legegyszerűbb út.
Vegyünk mondjuk egy OTP részvényt. Ennek ma a záróára 5270 Ft volt. Most az egyszerűség kedvéért legyen ez 3 Ft. A részvény ára minden nap végén általában más és más. Pl. tegnapelőtt még 4Ft volt, azelőtt megint 3Ft stb.. Az alábbi ábra kilenc napra visszamenőleg mutatja egy képzeletbeli részvény árának változását.

Néhány helyen ráírtam az értéküket is. Ma azaz jan 11-én, 3Ft- on zárt.
A kérdés a következő: Hogyan becsüljük meg a következő napi értéket (Jan 12) ?
Ha pusztán a fenti adatsorból próbálnánk meg a részvény következő napi értékét megbecsülni, akkor először természetesen adódik, hogy vonjunk átlagot a megelőző értékekből, de ez máris felvet egy újabb kérdést: hány értékből vonjunk átlagot? Az elmúlt egy évből, vagy csak az elmúlt kilenc napból? Nos, ez nagyrészt függ a tőzsde működésétől is. Általában egy évvel , vagy néhány hónappal ezelőtti értéke nem sokat számít bele a holnapi árba (pl. hogy egy hónappal ezelőtt volt-e nagyobb kiugrás egy-két napig ,az nem igazán számít), viszont a tegnapi vagy tegnap-előtti értékek annál inkább!
A példa kedvéért vegyünk egy négynapos átlagot. Ez azt jelenti, hogy a mai napi értéket úgy becsülöm, hogy átlagot vonok az elmúlt 4 napból, a holnapit úgy , hogy átlagot vonok az azt megelőző 4 napból stb..:
$$ F(n) \approx \frac{F(n-1) + F(n-2) + F(n-3) + F(n-4)}{4} $$
Itt F(n) az n. napi árat jelenti. A nagybetű arra utal, hogy F diszkrét függvény.
Amit itt láttok, annak a neve mozgó-átlag. Ahogy az látható, azért "mozgó",
mert visszamenőleg az adatsorból csak egy részhalmazt átlagolok: 4 napot, egy hónapot stb..
A fenti példa esetén a január 12-ei értéket igy számolom: F(jan12) ≈ (3+4+3+10)/4 = 5.
Pl. a február 5-ei értéket pedig így: (feb4 + feb3 + feb2 + feb1)/4 .
Észrevehető, hogy ugyanez könnyen felírható vektorok skaláris szorzataként is:
$$
F(\mbox{jan}12) \approx [0.25\quad 0.25 \quad 0.25 \quad 0.25 ] \cdot [3 \quad 4 \quad 3 \quad 10]
$$
(Itt 0.25-tel, azaz 1/4 -del szorozgatom végig, majd összeadom őket.)
Ha egy kicsit elgondolkodunk, akkor ez majdnem olyan, mintha két különböző "függvény"
elemeit látnánk magunk előtt, egyiknek az értékei a 0.25-ből álló vektor, a másiké pedig a
[3, 4, 3, 10] vektor és ezeket szorozgatnánk össze!
Próbáljuk meg egy kicsit általánosítani ezt az egészet! A fenti képen látható legelső kék diagram tehát F(n) képe.
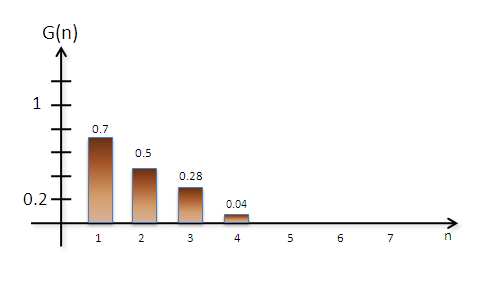
Egy másik függvény, G(n), pedig legyen a következő:
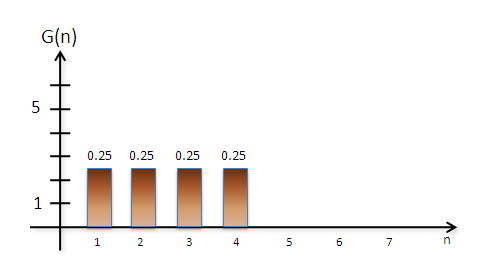
F(n) és G(n) legyen értelmezve
\$-\infty$\ -től
\$+\infty$\ -ig, és ahol a képeken
nincsenek ábrázolva ott mindenhol legyen 0 az értékük.
Azt kell észrevenni, hogy így van egy súlyfüggvényünk, G(n) , és van F(n) az "adatfüggvényünk".
Namármost, ezekkel a függvényekkel is leírhatjuk a fenti "átlagolást" (mozgó-átlag), amint azt a fenti skalárszorzásnál
láttuk. Legyen A(n) az n. napi becslés, - vagy átlag - az előző napokból, ekkor:
$$
A(n) = \sum_{k=1}^4\;G(k) \cdot F(n-k)
$$
Ami itt van az csak annyi, hogy egy n. napra úgy számolom ki az átlagot, hogy összeszorozgatom a
G(n) és F(n) megfelelő értékeit, majd
ezt a négy szorzatot összeadom..
A szumma 4-ig megy, mert G(n) ilyen "hosszú". Érdemes megfigyelni, h
ogy F paraméterként (n-k) -t kapott, azt jelenti , hogy ahogy k növekszik,
úgy "visszafelé haladunk" F -ben. Hogy miért
kell így csinálni az hamarosan kikristályosodik.
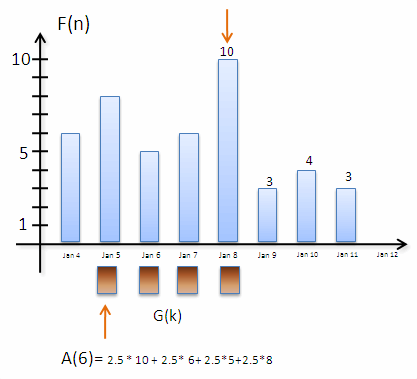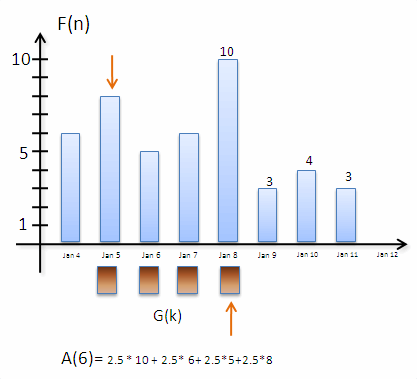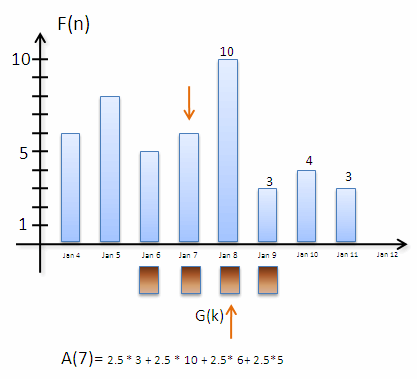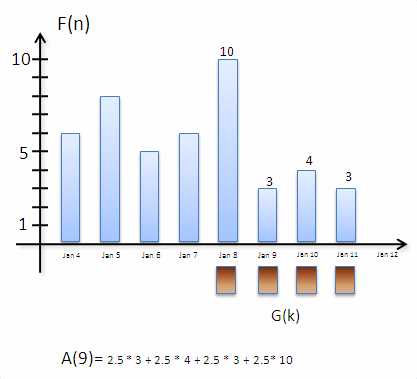
A következő animáció mutatja, hogyan működik a fenti képlet.
(Figyelem, az animáción 0.25 helyett véletlenül 2.5-öt írtam. Erre figyeljetek, mert megtévesztő lehet. Majd javítom a jövőben, elnézést érte.)
 Animáció elrejtése/megjelenítése
Animáció elrejtése/megjelenítése
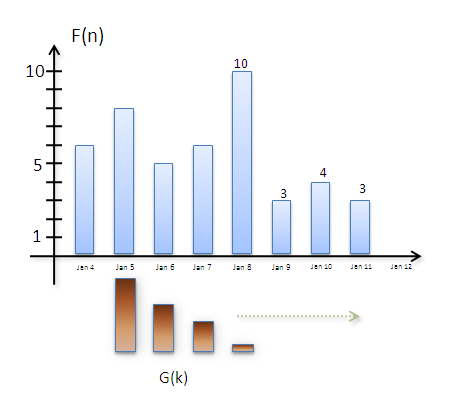
A képen egyszerre látható az F és G függvény. A G függvény hasonlóan az előző képhez barna szinű. Az animáció alsó részén látható az A(n) változása is, csak ez túl gyors lehet, ezért ide is kiírtam két lépést (valamint feltettem youtube-ra ott meg lehet állítani):
A(6)=0.25*10+ 0.25*6 + 0.25*5 + 0.25*8
A(7)=0.25*3 + 0.25*10 + 0.25*6 + 0.25*5
A piros nyilak mutatják mely értékeket szorzunk össze, lényegében ezek a nyilak
felelnek meg a feni szummában a k változásainak.
Itt látható ahogy "visszafelé haladunk" F ben. Ha megfordítanánk/tükröznénk a G függvényt,
akkor láthatóan a piros nyilak nem
haladnának egymással szembe, és talán könnyebb lenne elképzelni ezt ez egészet, ezért magyarázzák
úgy gyakran, hogy: "első lépésben tükrözzük a G-t"..
Látható, hogy az A(n) függvény -vagyis az n. nap "becslése"-, ahogy növeljük az n-et változik,és vele együtt
mozog a G függvény. Az n=1-nek a képen most Jan4 felel meg, n=5-nek pedig Jan 8.
Az animáció A(6)-tal kezdődik, azaz először Jan 9-ei értéket "becsüljük" meg.
Az is megfigyelhető, olyan mintha a G függvény "csúszna" az F függvényen. (Igazság szerint a
fenti képlet szerint úgy kéne az animációt csinálni, hogy az F függvény csússzon -a negatív
irányba- ,de úgy talán zavarosabb lett volna, illetve akkor a k nem 0 -től 4-ig menne.
A konvolúció kommutatív, magyarul mindegy melyik függvény "mozog", végül ugyanazt kapjuk,
de csak akkor ha a k
\$-\infty$\-től
\$+\infty$\ -ig megy .)
Amit így kapunk A(n)-re általában nem jó becslés. A G(n) függvény konstans -mindenhol 0.25- , ami azt jelenti, hogy a 4.nap (visszafelé számolva) is ugyanolyan súllyal számít be az átlagba mint a tegnapi nap. A tőzsdénél, -és sok más különböző helyen- a hozzánk közelebbi napok nagyobb súllyal szerepelnek. Ezért válasszuk úgy G(n)-et, hogy ne konstans, hanem egy exponenciális függvény legyen!
Az animáción is megfigyelhető volt, hogy először a G(n) "elejét" és az F(n) "végét" szorozzuk össze, majd ezután ellentétes irányba
haladunk. Magyarul, hogy jobb becslést kapjunk, úgy kell G(n)-et megválasztanunk, hogy a függvény eleje nagyobb legyen, majd a vége felé
csökkenjen.
Ezt teljesíti pl a következő függvény:
$$
G(n) = e^{-0.4n}
$$
A fenti animációban G(n) helyére ezt az "exponenciális" függvényt tesszük, ettől eltekintve minden ugyanúgy megy, ahogy fent. (A nyíl mutatja a G(n)
haladási irányát):
Talán sikerült megérteni ebből a diszkrét példából, hogy hogyan lehet eljutni egy ilyen "kibővített" átlagfogalom-ig. Nincs más hátra, mint áttérni folytonos függvényekre. Ekkor a szummából integrál lesz és a fenti egyenletből ez lesz:
$$ A(t) = (g * f)(t) = \int_1^4 g(\tau) \cdot f(t-\tau)d\tau $$ Itt a kisbetűk már a folytonos függvényekre utalnak. A konvolúciót gyakran (f*g)-vel vagy (g*f)-fel is jelölik.A következő kérdés még hátravan: általában a tau az integrálban -ellentétben a fenti képlettel- \$-\infty$\ -től \$+\infty$\ -ig megy , miért van ez ?
Egyrészt azért ,mert előre nem tudjuk, hogy az f és g milyen "hosszú". Másrészt lehet olyan eset mikor pl. a g függvény így néz ki: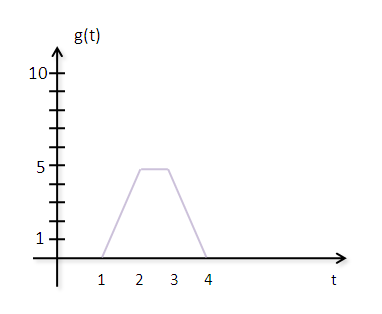
Ekkor úgy tekinthetünk g-re mintha több különálló függvényből lenne "összerakva", fel kell bontani az integrált, (először 1- től t-ig megy az integrálás majd 2-től 3-ig stb..), így a konvolúcós integrált (itt) háromszor kéne leírni: (valamilyen f függvényt odaképzelve)
$$ (g*f)(t) = \begin{cases} \int_1^t 5(\tau-1)\cdot f(t-\tau) d\tau & 1 \leq t \leq 2 \\\\ \;... &\\ \;... \end{cases} $$
Nem írtam le minden tagot. Majd néhány valós példán megpróbálom bemutatni, hogyan kell a konvolúciót kiszámolni, (az integrálási határokat felvenni stb..). A lényeg, hogy azért kell \$-\infty$\ -től \$+\infty$\ -ig integrálni, mert könnyebben le lehet írni/kevesebb helyet foglal. (A harmadik ok, hogy miért kell: ha nem végtelenig integrálnánk nem mindig teljesülne a kommutativitás, ezt egyszerű elképzelni, ha már megértettük a konvolúciót.)
Végeredményben tehát a konvolúció definíciója:
$$
(f*g)(t) \int_{-\infty}^{+\infty} f(\tau)g(t-\tau)d\tau
$$
vagy
$$
(g*f)(t) \int_{-\infty}^{+\infty} g(\tau)f(t-\tau)d\tau
$$
És a kommutativitás miatt ezek egyenlőek: (f*g)(t) = (g*f)(t).
A következő animáció a folytonos esetben mutatja a konvolúciót:
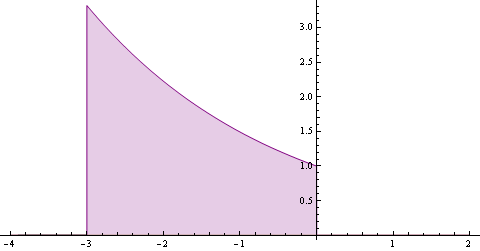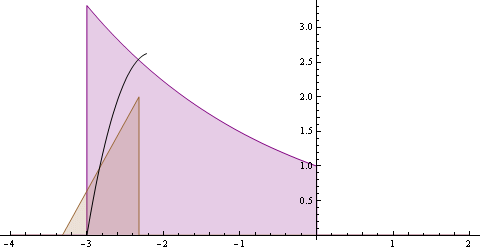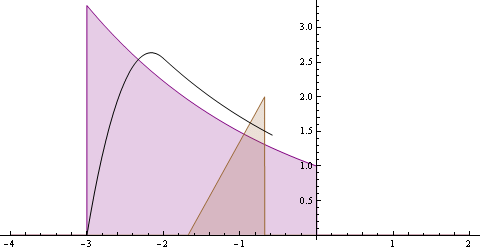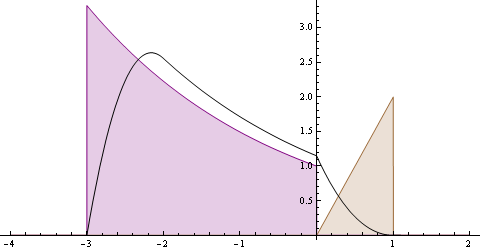 Animáció elrejtése/megjelenítése
Animáció elrejtése/megjelenítése
Az animáción a következő látható: A hátsó (nagy)lila függvény f, és a kisebb súlyfüggvény g, amelyik mozog. Illetve a fekete görbe, ami a (f*g)(t) értékét mutatja, és minden t pillanatban "frissül" ahogy g halad a t tengelyen. A függvények alatti területet a láthatóság kedvéért kiszíneztem. Az alábbi függvények vannak az animáción:
$$ f(t) = \begin{cases} e^{-0.4t} & ,ha \;-3 \leq t \leq 0\\ 0 & ,egy\acute{e}bk\acute{e}nt \end{cases} $$ $$ g(t) = \begin{cases} -2(t-1) & ,\;ha \;0 \leq t \leq 1\\ 0 & ,egy\acute{e}bk\acute{e}nt \end{cases} $$ $$ (f*g)(t) = \int_{-\infty}^{+\infty} e^{-0.4t} \cdot -2(t-\tau-1) d\tau $$ (Az f függvény most ugyanaz mint az előbb a diszkrét G(n) függvény , csak most folytonos és más az értelmezési tartomány). A g(t) függvény képe: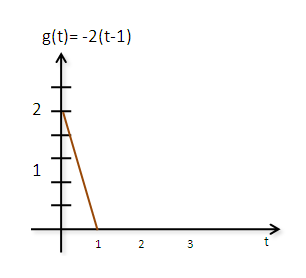
(Az animáción ez a függvény tükrözve jelenik meg.)
Azt, hogy hogyan kell konkrétan a konvolúciót kiszámolni különböző függvények esetén,
A konvolúciónak sok alkalmazása van, pl. gyakran használják arra, hogy "kisimítsanak" egy adott függvényt, tehát a kisebb eltéréseket eltüntessék belőle, kiszedjék a zaj egy bizonyos részét.. Most az animáción is talán kivehető, hogy a (g*f) függvény hasonlít az f függvényre, és hogy az f fenti "csúcsa" a (f*g)-n lekerekedik/kisimul. Persze ez a "simaság" tetszőlegesen változhat, attól függően milyen g súlyfüggvényt választunk.
Kapcsolódó cikkek:
Konvolúció példák

gongola
SZUPER!!!!
Ágnes
Nagyon jó cikk, érthető magyarázattal és igényes ábrákkal. Sokat segített, köszönöm szépen!
Dávid
Fantasztikus magyarázat, nagyon köszönöm! Örök hálám érte! :)
Miklos
Koszi, ertheto, es kulon koszi hogy vetted a faradsagot es csinaltal animaciokat!
filad
Köszönöm kedves Kérdező!
Kérdező
Jó oldal, csak gratulálni tudok hozzá. Az oktatási rendszerrel ellentétben a dolgok lényegét mutatja be úgy, ahogy és amiért azokat megalkották és nem a mindezt eltakaró elegáns, de semmitmondó matematikai megközelítést.
Két dolog szúrt szemet:
$$
(g*f)(t) =
\begin{cases}
\int_1^t 5(\tau-1)\cdot f(t-\tau) d\tau & 1 \leq t \leq 2 \\\\
\;... &\\
\;...
\end{cases}
$$
itt a leírás szerint 4-szer kell integrálni, ez nem világos, hiszen ha úgy nézzük, 3 függvénnyel lehet definiálni azt a "trapéz" alakú függvényt.
---
itt viszont mintha az exp. fv. argumentuma lekerült volna szorzótényezőnek:
$$ (f*g)(t) = \int_{-\infty}^{+\infty} e{-0.4t} \cdot -2(t-\tau-1) d\tau $$
Hl55
Nagyon hasznos cikk,segített a záróvizsga felkészülésben,Köszönöm
CH Andras
Szuper cikk! Sokkal érthetőbbe tette számomra a konvolúció fogalmát. Köszönöm!
filad
@cirmoscica
Good call. Minnél hamarabb kijavítom.
cirmoscica
ahol a nyilak dancelnek, ott 2.5-tel van szorozva alul minden 0.25 helyett, ami elég félrevezető lehet.
S. Józsi
Köszönöm szépen a részletes leírást! Számomra nagyon hasznos volt!
filad
@Gábor
Köszönöm visszajelzésed, majd rakok bele néhány kiegészítést ezzel kapcsolatban.
Gábor
Nagyon jó leírás, csak gratulálni tudok hozzá.
Viszont nálam nem kristályosodott ki, miért halad visszafele a súlyfüggvény. Erről ha lehetne még kicsi kiegészítés az nem volna rossz.