A legtöbb atommagnak megvan az a tulajdonsága,
hogy bármiféle külső hatás nélkül egy részecskét kibocsát és
másik atommaggá alakul át. Ezek a magok radioaktívak, a folyamatot
radioaktív bomlásnak nevezzük. A radioaktív bomlás folyamata véletlenszerű, statisztikus jelenség.
Mivel a radioaktív bomlás statisztikus jelenség, arra következtethetünk,
hogy lehetetlen megmondani, mikor fog a radioaktív anyag valamelyik atomja bomlani,
de méréssel meg lehet határozni, hogy mennyi ideig tart átlagosan, amíg a vizsgált minta radioaktivitása a felére csökken.
Az átalakulás időbeli lefolyását a felezési idővel jellemezhetjük.
Azt az időt, amely alatt egy radioaktív anyagban a radioaktív magok száma a kezdeti érték felére csökken, felezési időnek nevezzük. A felezési idő jellemző az adott izotópra. A különböző radioaktív anyagok felezési ideje a tízmilliárd évtől a másodperc milliárdod részéig terjedhet.
Általában ún. stabil magoknak tekintik azokat, melyek felezési ideje a világegyetem feltételezett koránál nagyobb, és instabil radioaktív magoknak azokat, melyek felezési ideje ennél kisebb.
Annak a valószínűsége, hogy egy kiszemelt atommag \$T_{1/2}$\ idő alatt elbomlik (\$T_{1/2}$\ a felezési idő) éppen 1/2. Újabb \$T_{1/2}$\ idő alatt bekövetkező bomlás valószínűsége ismét 1/2, attól függetlenül, hogy az atommag mióta "vár" már a bomlásra.
A bomlásállandót (\$\lambda$\) a következőképpen értelmezzük: annak a valószínűsége,
hogy egy kiszemelt atommag egységnyi idő (pl. 1s) alatt elbomoljon,
éppen \$\lambda$\.
Miután ez egy kiszemelt atommag-fajtára időben állandó,
képletesen azt is mondhatjuk, hogy az atommagok "nem öregszenek", hiszen az elbomlásuk
minden időpillanatban ugyanolyan valószínűségű, függetlenül attól, hogy már mennyi ideje léteznek.
(Az élőlényeknél ez másként van...) Ebből az egyszerű feltételezésből az exponenciális bomlástörvény "levezethető":
Ha \$\lambda$\ annak a valószínűségsűrűsége, hogy egyetlen atommag időegység alatt elbomoljon, akkor nyilván az illető atommag \$dt$\ idő alatt \$\lambda \cdot dt$\ valószínűséggel bomlik el. Azt, hogy egy kiszemelt atommag pontosan mikor fog elbomlani, nem lehet megmondani, de ha nagy számú atommagot vizsgálunk, akkor meg lehet mondani, hogy a nagyon sok közül átlagosan hány bomlik el dt idő alatt: \$N \cdot \lambda \cdot dt$\. Ennyi idő alatt tehát ennyivel csökken a meglévő atommagok száma, azaz az atommagok számának \$dN$\ megváltozása: \$dN = - N \cdot \lambda \cdot dt$\. (A negatív előjel azt fejezi ki, hogy az atommagok száma csökken.) Ez az egyenlet összefüggést ad az atommagok számának megváltozása és a meglévő \$N$\ szám között: $$\frac{dN}{dt} = - \lambda \cdot N(t)$$ Ez egy ún. differenciálegyenlet, mert szerepel benne egy függvény - az \$N(t)$\ - és annak a megváltozása, deriváltja is \$\frac{dN}{dt}$\. Ilyen jellegű differenciálegyenlettel nagyon gyakran találkozunk nemcsak a fizikában, de más természeti jelenségek leírása során is (pl. biológiában egyes populációk növekedése, kémiában egyes reakciók lefolyása stb.). Ennek a differenciálegyenletnek a megoldása egy exponenciális függvény: $$N(t) = N_0 \cdot e^{-\lambda t}$$
Az \$N_0$\ konstans értelmezése: a függvény értéke a \$t = 0$\ kezdeti időpontban
(a mi esetünkben a kezdetben meglévő radioaktív atommagok száma).
Ennek az időfüggvénynek a menetét mutatja az alábbi ábra.
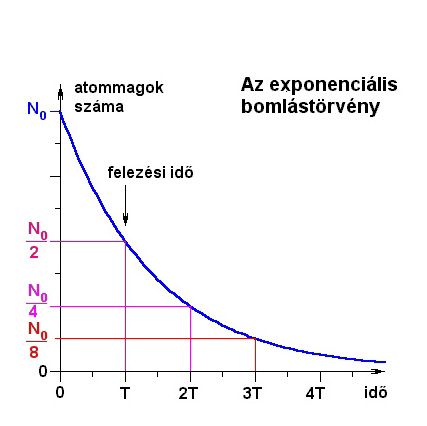
Ez az exponenciális bomlástörvény egyik alakja. Egy másik, gyakran használt alakot úgy kapunk meg, ha az "e" alapról ( = 2,718281828459..., a természetes logaritmus alapszáma) 2-es alapra térünk át:
$$ N(t) = N_0 \cdot 2^{-\frac{t}{T}} $$Az ebben az alakban szereplő \$T$\ - felezési idő és az előző képletben szereplő \$\lambda$\ (egységnyi időtartamra eső bomlási valószínűség) nem függetlenek egymástól: $$T = \frac{ln 2 }{\lambda} = \frac{0.693147}{\mu}$$
Minden radioaktív anyag esetén a felezési idő állandó. A bomlások miatt fogy a radioaktív magok száma. Ebből arra következtethetünk, hogy azonos idő alatt kevesebb bomlás következik be. Az adott anyag radioaktivitása csökken. Ezt számszerűen az aktivitással fejezhetjük ki.
Egy adott radioaktív anyag aktivitásán az időegység alatt bekövetkezett bomlások számát értjük. Jele: a. Mértékegysége bomlás/s, amelyet Becquerel emlékére becquerelnek (Bq) neveznek.
Az aktivitás régi egysége a curie (ejtsd: küri).
Az aktivitás időbeli változására a felezési időhöz hasonló függvény adhat meg: $$ a(t) = a_0 \cdot e^{-\lambda t}$$
Radioaktív forrás aktivitása egyenesen arányos az anyagban lévő, bomlásra képes (még el nem bomlott) atommagok számával \$N$\ : $$ a = \lambda N$$ Mégegyszer: a \$\lambda$\ neve bomlásállandó. Mértékegysége 1/s.

0 Komment