Green-tétel (vektoranalízis)

Ebben a cikkben a vektoranalízisben használt Green-tételről fogok néhány szót írni (amit úgy is hívnak, hogy "síkbeli Stokes-tétel", ugyanis a Stokes-tétel egyik alesetéről van szó).
Megpróbálom megmutatni, hogy intuitíven hogyan lehet ehhez a tételhez eljutni. Ez nem bizonyítás, csak egyfajta "szemléletes megközelítése" a dolgoknak, a pontos bizonyítás a legtöbb analízis tankönyvben le van írva.

Ha van egy irányított zárt görbénk C , akkor ezen a görbén értelmezett vonalintegrál: $$ \int_C \mathbf F \cdot d\mathbf s $$ jelenti a vektormező ún. "cirkulációját" a görbe mentén. Ez azt "méri", hogy a vektormező mennyire forog körbe a görbe vonalán (a vektormező vektorai mennyire esnek a görbével egyirányba).
(Erről itt is olvashatsz: A vonalintegrál, mint cirkuláció.)
A C görbénk itt látható:

A probléma az, hogy gyakran igen nehézkes a fenti vonalintegrált kiszámolni. Itt jön majd a képbe a Green-tétel.
Ha két dimenzióban vagyunk, és a görbe zárt (a kezdőpont megegyezik a végponttal), akkor felhasználhatjuk a Green-tételt mint egy alternatív módszert a vonalintegrál kiszámolására.

A Green-tétel csupán annyit csinál, hogy áttranszformálja a C menti vonaltintegrált a C által körülzárt területre vett kettős integrállá.
A kérdés az, hogy így a kettős integrálban milyen függvény szerepel, ami ugyanazt az eredményt fogja adni mint a sima vonalintegrál?

Az \$\displaystyle \int_C \mathbf F \cdot d\mathbf s$\ vonalintegrálra (azaz a cirkulációra) lehet úgy gondolni, mint az F vektormező "MAKROszkopikus" cirkulációjára a C mentén. (Erről volt szó pl. a Makro vs. mikroszkopikus cirkuláció részben)
Ezzel szemben a "mikroszkopikus" cirkuláció - ahogy a nevéből is látszik - egy kis pontszerű cirkulációt jelent egy (x,y) pont körül (kis területegységre eső cirkulációt).
A mikroszkopikus cirkulációt ábrázolhatjuk az egyes pontokban úgy, mintha végtelenül kicsi zárt görbéket vennénk fel. Ezek a zárt görbék pedig az ottani lokális (pontbeli) cirkulációt adnák meg.

A Green-tétel kapcsolatot teremt a MAKRO- és a mikroszkopikus cirkulációk között, mégpedig: a mikroszkopikus cirkulációk összege kiadja a C görbére vett teljes (MAKROszkopikus) cirkulációt.

Vizsgáljuk meg ezt az egészet egy kicsit érthetőbben.
Ha C tehát egy zárt görbe a síkon (emlékezz, most csak 2 dimenzióban vagyunk), akkor ez a görbe körülvesz valamekkora területet. A képen D-vel jelöltük.

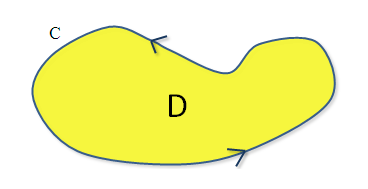
A Green-tétel azt mondja, ha összeadjuk ezeket a kis mikroszkópikus cirkulációkat D-n belül, akkor megkapjuk a C görbére vett teljes (MAKROszkópikus) cirkulációt. Magyarul megkapjuk a C-re vett vonalintegrált.

"Összeadni" a D-beli mikroszkopikus cirkulációkat annyit tesz, hogy integráljuk őket a D-n.
A Green-tétel tehát következőt fejezi ki:

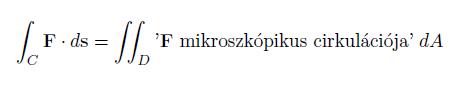
Namost, matematikailag hogyan adjuk meg az "F mikroszkopikus cirkulációját"?
A válasz röviden: a rotáció segítségével. A rotációról tudjuk, hogy éppen ezt a fajta mikroszkopikus cirkulációt "méri" az egyes pontokban. A Green-tétel persze csak két dimenzióban igaz. Ezért a görbét most az xy síkra képzelve, jelen esetben csak a rotáció z-komponensére van szükségünk. (A rotáció komponenseit ismerve ez nem is meglepő.)

Így a Green tétel esetében:

"mikroszkopikus cirkuláció" = (rot F)·k
(, ahol k a z-tengely irányába mutató egységvektor.)
Ez az egyenlőség annyit jelent mégegyszer, hogy a "mikroszkopikus cirkulációkat" az egyes pontokban - azaz amit integrálni kell a D régión (kis zöld vonalintegrálokat a képen)- a rotáció z-komponense adja meg , mivel csak az xy síkon vagyunk.
Mindezek után így építhetjük tovább az egyenlőséget:

$$ \int_C \mathbf F\cdot d \mathbf s = \iint_D (rot \mathbf F) \cdot \mathbf k \; d\mathbf A $$

Ha visszatekintesz a rotációra, akkor látod, hogy a harmadik (z-irányú) komponense a következő volt:

$$ (rot \mathbf F) \cdot \mathbf k = \frac{\partial F_2}{\partial x} - \frac{\partial F_1}{\partial y} $$ Végül tehát a Green tételt így írhatjuk: $$ \int_C \mathbf F\cdot d \mathbf s = \iint_D \left( \frac{\partial F_2}{\partial x} - \frac{\partial F_1}{\partial y} \right) \; dA $$

A rotációnál ugye a jobbkéz szabály szerint járunk el, emiatt akkor lesz "pozitív" az integrál, ha az xy-síkon fekvő mikroszkopikus cirkuációk -és maga a görbe is- az óramutató járásával ellentétes irányba haladnak. Ellenkező esetben - ha a görbe az óramutatóval megyező irányítású- az egész kap egy negatív előjelet.
(Megj.: A C görbe a D-nek ún. pozitív határvonala, ami azt jelenti, hogy C úgy van irányítva, hogy rajta sétálva mindig a bal oldalon legyen D terület. Ez majd ott jön elő igazából, amikor a D-nek több határa van.)

Találhatsz még néhány mondatot a Green tétel alternatív jelölésmódjaival kapcsolatban. Illetve, amit itt tárgyaltunk az még nem minden, ugyanis a Green tétel olyan D régiókra is alkalmazható amelyben vannak "hézagok".

Green tétel összefoglalás

A továbbiakben mégegyszer leírom, hogy milyen feltételek esetén lehet a Green tételt alkalmazni; éppen azért, mert gyakran akkor is használják amikor nem kéne (mert nem állnak fenn ezek a feltételek).

A Green tétel tehát ad a kezünkbe egy másik utat a $$ \int_C \mathbf F\cdot d \mathbf s $$ vonalintegrál kiszámolására. A Green tétel csak akkor "működik" ha a C egy zárt görbe, ellenkező esetben nem lehet használni!

Ha a fenti intuitív levezetésre gondolsz, akkor nem fogod elrontani, hogy mikor lehet használni a Green tételt. A tétel ugye "átkonvertálja" a vonalintegrált a mikroszkopikus cirkulációkon értelmezett kettős integrállá. Ezt a kettős integrált a D-n (körbezárt területen) értelmeztük, egy nyílt görbe viszont nem zárhat körül egy területet.

Pl. ki kell számolnod a következő vonalintegrált: $$ \int_C (y \;dx + xy \; dy) $$
, ahol a görbe (0, 1)-től (1, 1)-ig megy. Használhatod-e a Green-tételt a vonalintegrál kiszámolására? Nem, mert a görbe nem zárt.
Ha a görbe most pl. az egységkör lenne, az óramutató járásával ellentétes irányítással, akkor már lehetne használni a Green tételt.

A másik dolog pedig: A Green tétel csak két dimenziós vektormezőknél alkalmazható. Mint pl. F(x,y) = (y, xy) a fenti példában. Háromdimenziós vektormezőknél nem használható.
Tehát ha kapsz egy ilyen vonalintegrált:
$$ \int_C (z \;dx + xy\;dy - yz\;dz) $$
, akkor a Green-tételt nem lehet alkalmazni.
Néhány konkrét példát olvashatsz itt a Green tétellel kapcsolatban

Kapcsolódó:
- Mikroszkopikus vs. makroszkopikus cirkuláció különbség a rotáció és a "normális" cirkuláció között.
- A vonalintegrál egyéb jelölésmódjai
- A vonalintegrál, mint "cirkuláció"

- A Green tétel "hézagok" esetén