Felületi integrál (animációval)

A görbék és a felületek közt sok hasonlóság van.

Emlékezz rá, hogy a görbéknél kétfajta vonalintegrált is értelmezünk: az egyiket valós függvényen, a másikat pedig vektormezőn.
Ugyanígy, a felületek esetében is lehet valós-függvényen, illetve vektormezőn értelmezett felületi integrálról beszélni.

Felületi integrál valós-függvényen

Legyen egy felületünk, Φ(u,v), valamilyen D értelmezési tartományon.

Egy felület felszínének kiszámolásakor úgy jártunk el, hogy felosztottuk a felületet kis felületdarabokra, majd ezeknek a területeit "összeadtuk" (integráltuk).
Egy kis felületdarab területe a következő volt: $$ \left\|\frac{\partial \mathbf{\Phi} }{\partial u}(u,v) \times \frac{\partial \mathbf{\Phi} }{\partial v}(u,v)\right\| \;du \; dv $$
(erről volt szó pl az egységnyi felületelem felszine részben.)
A teljes felület tehát: $$ A = \iint_D \left\|\frac{\partial \mathbf{\Phi} } {\partial u}(u,v) \times \frac{\partial \mathbf{\Phi} }{\partial v}(u,v)\right\| \;du \; dv $$

Namost gyakran szükség van arra, hogy ezeket a felületdarabokat valamilyen számmal szorozzuk, és így összegezzük őket. Azt, hogy milyen számmal szorozzuk egy f(x,y,z) függvény adja meg:
(1) $$ \iint_D f(\mathbf{\Phi}(u,v))\cdot\left\|\frac{\partial \mathbf{\Phi} } {\partial u}(u,v) \times \frac{\partial \mathbf{\Phi} }{\partial v}(u,v)\right\| \;du \; dv $$ Ez pedig nem más mint a felületi integrál valós-függvényen. Semmi mást nem csináltunk csak az előbbi formulát egy f(Φ(u,v))-el bővítettük. Itt Φ(u,v) felület egy (x,y,z) pontját jelenti, pl Φ(u,v)= (2u, sin v, v).
Látható, hogy ha f(x,y,z)= 1 konstans, akkor egyszerűen visszakapjuk a fenti területet.

Mikor használjuk ezt?
Egy tipikus példa, hogy minden felületdarabnak van valamennyi sűrűsége, f(x,y,z). Tehát pl. a (3,4,8) pontban f(3,4,8) = 2.6 g/cm².
Szeretnénk megmondani a teljes felület tömegét.
Egy kis felületdarab "tömege", az ottani sűrűség f(Φ(u,v)) szorozva a felületdarab területével, amit már ismerünk.
(ugye most a sűrűség szer terület egyenlő a tömeggel: g/cm²∙cm²=g) Tehát egy kis felületdarab tömege a következő: $$ f(\mathbf{\Phi}(u,v))\cdot\left\|\frac{\partial \mathbf{\Phi} } {\partial u}(u,v) \times \frac{\partial \mathbf{\Phi} }{\partial v}(u,v)\right\| \;du \; dv $$ , és ezt kell végigintegrálni ahhoz hogy a teljes tömeget megkapjuk, ahogy azt az (1) formulában láttuk.

Megjegyzés:
Ez a kettős integrál lényegében két-dimenziós analógja a görbéknél már látott valós-függvény vonalintegráljának, azt kivéve, hogy itt IIΦ'(t)II helyett most a $$ \left\|\frac{\partial \mathbf{\Phi} } {\partial u}(u,v) \times \frac{\partial \mathbf{\Phi} }{\partial v}(u,v)\right\| $$ kifejezés szerepel.

Felületi integrál vektormezőn

Kanyarodjuk vissza újra a görbékhez. A görbéknél látott vektormező vonalintegrálja szemléletesen azt adta meg, hogy a vektormezőnek mennyi munkát kell végeznie mialatt pl. egy részecske végigmegy az adott görbén.
A felületi integrálhoz is rendelhetünk egy szemléletes képet, bár ez különbözik a vonalintegrálnál látottól. A felületi integrál itt nem a vektormező munkájáról ad információt, hanem arról hogy a megadott felületen mennyi folyadék áramlik keresztül, egységnyi idő alatt. (Ha a vektormező folyadékot reprezentál.)

Egy felületen, egységnyi idő alatt átáramló folyadék mennyiségét a folyadék (adott felületre vett) fluxusának is hívjuk.
("Valaminek" a fluxusa megadja, hogy ebből a "valamiből" ami lehet folyadék, levegő.., egy adott felületen mennyi áramlik át egységnyi idő alatt. Pl. kg/s, db/s, vagy energia esetén J/s. *)

Maradjunk a folyadéknál... A lényeg tehát, hogy a felületi integrál egyenlő a fluxussal.

Lépjünk tovább, és nézzük meg, hogy ez a fluxus (tehát felületen átmenő folyadékmennyiség) mikor lesz nagy.
Akkor lesz nagy, ha a felület merőleges a folyadék áramlására. Ellenben ha a felület párhuzamos a folyadék áramlásával, akkor nem fog átáramlani rajta semmi, a fluxus nulla lesz. Ez látható a képeken:

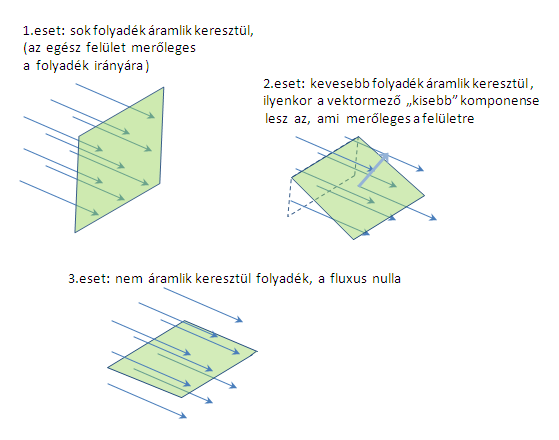itt a kék vektorok az F vektormezőt ábrázolják.

Ha ezek után van egy tetszőleges felületünk (ami nem feltétlenül síkfelület), akkor ennek ugye minden pontban van egy normálvektora n. Ez a normálvektor az ottani kis felületdarabra merőleges. Ez a kis felületdarab látható alul zölddel a bal oldalon (a téglalap gondolatban végtelenül kicsi). Belerajzoltam a normálvektort is (feketével). A jobb oldalon pedig ugyanez, csak lecsupaszítva, itt látható amire nekünk szükségünk van: F azon komponense ami n irányba mutat (kis kék vektor), magyarul a vektormező azon része amely merőleges az ottani felületdarabra:

A felületi integrál annyit csinál, hogy összeadja a vektormező n irányú részeit (magyarul, a képen a "kis kék" vektorokat). Így megkapjuk , hogy a felületen mennyi folyadék áramolhat keresztül összesen.

Az F azon komponenseit amelyek az n irányába mutatnak az F•n skaláris szorzat adja meg (n a normál egységvektor).
(Megjegyzés: Figyeld meg, hogy most éppen azt szeretnénk "megmérni", hogy F és n mennyire mutatnak egyirányba az adott pontban, már volt szó róla, hogy a skaláris szorzat éppen erről szól.)

Próbáljuk meg illusztrálni ezt az egészet egy kicsit konkrétabban. A felület legyen a már ismert ún. csavar-felület. A normálvektor most kék színű.

Java animáció megjelenítése / elrejtése (nem minden böngésző támogatja már)

Adva van valamilyen folyadékáramlás F, ami most magenta színű vektorokkal van jelölve:

Java animáció megjelenítése / elrejtése (nem minden böngésző támogatja már)

A fenti animációból is lehet látni, hogy a folyadék iránya és a normálvektor iránya valahol jobban megegyezik, valahol kevésbé. Ez pontonként változik.
Pl. amikor s = 0 és t = 2π, akkor F ellenkező irányba folyik, mint n, ebben a pontban negatív lesz majd a skaláris szorzat.

Az alsó animáció talán világosabban mutatja a fentieket. Itt láthatod mégegyszer, amint együtt van az F (magenta), és a normálvektor (kékkel) a felület egyes pontjaiban .
Az aktuális F•n szorzat értékét az oldalsó kék slider-en ábrázoltam. Itt is megfigyelhető, hogy F•n nagyrészt pozitív lesz, néhány helyen pedig negatív. Ahol pedig az F•n = 0, ott mi is van? (A választ a kedves olvasóra bízom...na jó, megsúgom: ott F és n merőlegesek egymásra, azaz a folyadékáramlás és a normálvektor merőleges ilyenkor ugye nem folyik át a felületen semennyi folyadék abban az adott "pontban", jéé és a skaláris szorzat ennek megfelelően itt éppen 0 lesz!)

Java animáció megjelenítése / elrejtése (nem minden böngésző támogatja már)

Most tehát annyi a dolgunk, hogy a valós függvénynél látott (1) formulát alkalmazzuk az F•n -re (mert ez az F•n skaláris szorzat lényegében egy valós függvény, tehát az egészet leredukálhatjuk a cikk első felében látott valós fv. vonalintegráljára).

$$ \iint_S \mathbf F \cdot d\mathbf S = \iint_S \mathbf F \cdot \mathbf n\; dS = \iint_D (\mathbf F \cdot \mathbf n) \left\| \frac{\partial \mathbf \Phi} {\partial u} \times \frac{\partial \mathbf\Phi}{\partial v} \right\| \;du \; dv $$

A felület normál egységvektora - n - így nézett ki:

$$ \textbf{n}= \frac{\dfrac{\partial \mathbf{\Phi} }{\partial u}(u,v) \times \dfrac{\partial \mathbf{\Phi} }{\partial v}(u,v)}{\left\| \dfrac{\partial \mathbf{\Phi} }{\partial u}(u,v) \times \dfrac{\partial \mathbf{\Phi} }{\partial v}(u,v)\right\|} $$ amit ha behelyettesítünk az előbbi formulába, akkor a \$\dfrac{\partial \mathbf{\Phi} }{\partial u}(u,v) \times \dfrac{\partial \mathbf{\Phi} }{\partial v}(u,v)$\ tagok kiejtik egymást, és ezt kapjuk: $$ \iint_S \mathbf F \cdot d\mathbf S = \iint_D \mathbf F(\mathbf \Phi(u,v)) \left(\dfrac{\partial \mathbf{\Phi} }{\partial u}(u,v) \times \dfrac{\partial \mathbf{\Phi} }{\partial v}(u,v) \right) \;du \;dv $$

,és ez lesz a végső alakja a vektormezőn értelmezett felületi integrálnak.

Figyeld meg, hogy mennyire hasonlít a görbe vonalintegráljára, az így nézett ki:

$$ \int_C \mathbf F \cdot d\mathbf s = \int_a^b \mathbf F(\mathbf c(t)) \cdot \mathbf c'(t)\; dt $$

A vonalintegrálnál a vektormező azon komponenseit integráltuk amelyek érintőirányba mutattak a görbén, (az érintőirány c'(t) volt). Most a felületi integrálnál pedig a normál irányú (felületre merőleges) komponenseket integráljuk. A felületre merőleges irány ugye a \$ \left(\dfrac{\partial \mathbf{\Phi} }{\partial u}(u,v) \times \dfrac{\partial \mathbf{\Phi} }{\partial v}(u,v) \right)$\ volt.

Néhány példát találhatsz itt

*A fluxust különböző területeken néha máshogy is értelmezik, de most ebbe nem akarok belemenni részletesen.