Most nézzuk meg, hogyan lehet kiszámolni egy egységnyi felületelem nagyságát.
Ezt majd felhasználjuk a teljes felület
felszínének tárgylásakor is.
A továbbiakban az "egységnyi felületelem" egy végtelenül kicsi felületdarabot jelöl.
Tegyük fel, hogy van egy felületünk, Φ(u,v), valamilyen D értelmezési tartományon. Ekkor úgy is beszélhetünk Φ-ről, mint ami "áttranszformálja" D-t (ami egy síkfelület) valamilyen módon (pl. 3D-s felületté).
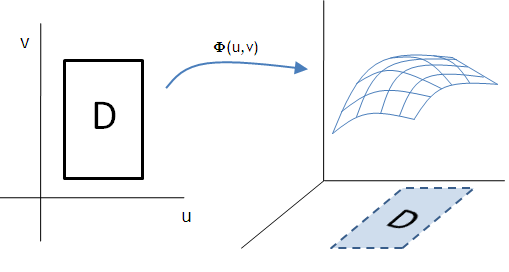
Ahogy az előzőekben most is feloszthatjuk a D-t kis téglalapokra, és megnézhetjük, hogy egy ilyen kis téglalapnak mi lesz a képe Φ(u,v)-ben.
A következő ábrán látható, amint Φ a bal oldali kis D-beli téglalapot egy ilyen térbeli "görbült oldalú kis téglalappá" (a felület egy darabjává) képezi le. (A jobb oldalon a felület egy "darabja" látható.)
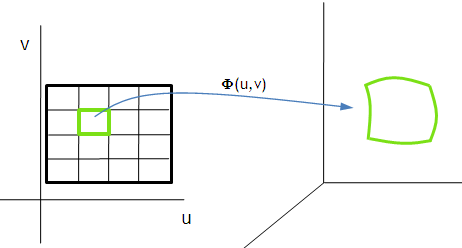
Legyen ennek a D-beli kis téglalapnak a hossza Δu, magassága pedig Δv. Hogyha a téglalap bal alsó sarka
az (u,v) pontban van, akkor Φ ezt a pontot a Φ(u,v) pontba fogja leképezni.
(Tehát Φ(u,v)
lesz a kis "görbe téglalap" bal alsó pontja)
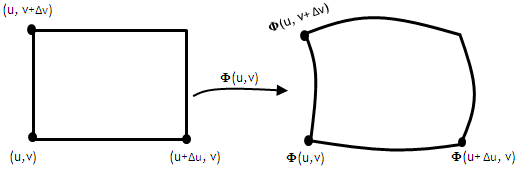
A jobb alsó sarok ,(u + Δu, v), pedig a Φ(u + Δu, v) pontba fog kerülni a felületen.
A kérdés az, hogy mennyi a területe ennek a kis "görbe téglalapnak"?
Ha kicsi Δu és Δv akkor közelíthetjük egy paralelogrammával (az alsó képen téglalap van). Minnél kisebb Δu és Δv a "görbültség " annál jobban eltűnik , és annál jobb lesz a közelítés.
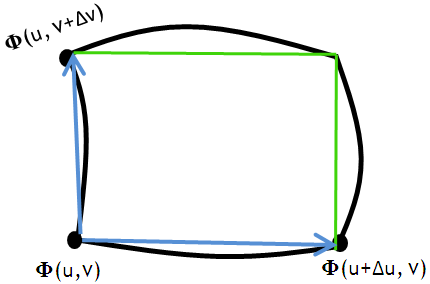
Itt látható amint ezt a "görbe téglalapot" egy paralelogrammával (itt téglalappal) közelítjük, amit a kék vektorok "feszítenek ki". Ennek a téglalapnak a területére vagyunk kíváncsiak minnél kisebb Δu, Δv mellett.
Ennek a paralelogrammának az egyik oldala:
$$ \begin{align} \mathbf{\Phi}(u+\Delta u, v)-\mathbf{\Phi}(u, v) &= \frac{\mathbf{\Phi}(u+\Delta u, v)-\mathbf{\Phi}(u, v)}{\Delta u} \cdot \Delta u\\ &\approx \frac{\partial \mathbf{\Phi}}{\partial u}(u, v) \Delta u \end{align} $$ Itt az első tag Φ(u+Δu, v) - Φ(u,v): a Φ(u,v) pontból a Φ(u + Δu, v) pontba mutató vektor (kékkel jelölve az ábrán).A másik oldal (vektor) pedig:
$$ \mathbf{\Phi}(u, v+\Delta v)-\mathbf{\Phi}(u, v) \approx \frac{\partial \mathbf{\Phi}}{\partial v}(u, v) \Delta v $$A két vektor által "kifeszített" kis téglalap területe pedig: a vektoriális szorzatuk abszolút-értéke.
$$ \left\|\frac{\partial \mathbf{\Phi} }{\partial u}(u,v) \times \frac{\partial \mathbf{\Phi} }{\partial v}(u,v)\right\| \;\Delta u \Delta v $$
Ez lesz tehát egy kis felületelem - kis "görbe téglalap"- felszíne.
(Közelítőleg. Δu és Δv minnél kisebbek annál jobb a közelítés.)
Az egész felület teljes felszíne pedig majd ezeken a kis téglalapokon értelemezett Riemann-összeg lesz. Ha vesszük a Δu, Δv → 0 határértékeket, akkor a Riemann-összeg egy kettős integrálhoz konvergál, végül azt kapjuk, hogy a kis téglalapokból összerakott teljes terület pedig:
$$ A = \iint_D \left\|\frac{\partial \mathbf{\Phi} }{\partial u}(u,v) \times \frac{\partial \mathbf{\Phi} }{\partial v}(u,v)\right\| \;du \; dv $$ amiől a bevezetőben is linkelt felület felszíne részben olvashatsz.
filad
A következő kifejezést:
$$\approx \frac{\partial \mathbf{\Phi}}{\partial u}(u, v) \Delta u $$
el is lehetett volna hagyni. Nincs mélyebb mondanivalója.
Ha megnézed ott van egy "\$ \approx $\" (közelítő) jel.
Ezzel csak azt akartam mutatni, hogy a
$$\frac{\mathbf{\Phi}(u+\Delta u, v)-\mathbf{\Phi}(u, v)}{\Delta u} \approx \frac{\partial \mathbf{\Phi}}{\partial u}(u, v)$$
Tehát a baloldali tört a parciális deriváltat közelíti ha kicsi a \$\Delta u$\.
Szóval ez csak egy matematikai közelítés, nem éredemes semmilyen képet rendelni hozzá, mert csak zavarosabb lesz:)
dterbe
Egy kicsit nehéz felfogású vagyok, így nem teljesen tiszta a következő rész jelentése számoma:
\$\begin{align}
\mathbf{\Phi}(u+\Delta u, v)-\mathbf{\Phi}(u, v) &= \frac{\mathbf{\Phi}(u+\Delta u, v)-\mathbf{\Phi}(u, v)}{\Delta u} \cdot \Delta u\\
&\approx \frac{\partial \mathbf{\Phi}}{\partial u}(u, v) \Delta u
\end{align}$\
Értem az átalakításokat és a trükköt, de ennek nincs valami érthető mondanivalója? Én valahogy így látom: A parciális derivált tag megadja az adott irányba lévő meredekséget (de ez nem skalár érték? ha nem skalár hanem vektor, akkor az iránya érintő irányú és nagysága a meredekség nagysága, vagy egység nagyságú?) egységvektorként, tehát irányt ad és a delta u pedig nagysággal ruházza fel ezt a vektort.
De úgy érzem (inkább biztos vagyok benne) hogy ez nem így van. Kicsit kavarom a dolgokat. Remélem érthető a problémám és talán mások számára is segít érthetőbbé tenni ezt az egészet.