Néhány konvolúcióval kapcsolatos példa.
1.példa
Kezdjük egy egyszerű példával.
Számoljuk ki a következő függvények konvolúcióját:
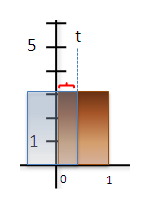
Namost miért kell 0-tól t-ig integrálni?
Mert ha elképzeljük, amint a g függvény halad az x-tengelyen,
(magyarul
az (f*g)(t) ben a t egyre növekszik), úgy a g egyre jobban lefedi az f-et. Mindig addig integráljuk őket amíg a két
függvény fedi egymást.
Ha a t pedig 1 és 2 között mozog, akkor (f*g)(t): $$ \begin{eqnarray} (f*g)(t) & = & \int_{t-1}^{1}3\cdot3\;d\tau = 18-9t \qquad \qquad 1 \leq t\leq 2 \;eset\acute{e}n \end{eqnarray} $$
Az elhaladó függvény egyre kisebb területet "fed le", az integrál t-1 től 1-ig halad, majd miután elhagyja az 1-et (f*g)(t) nulla lesz. Hogy most miért kell t-1 től integrálni az elég nyilvánvaló. Mert a mozgó g függvény "szélessége" egy egységnyi. (Aki esetleg nem érti, írhat kommentben)
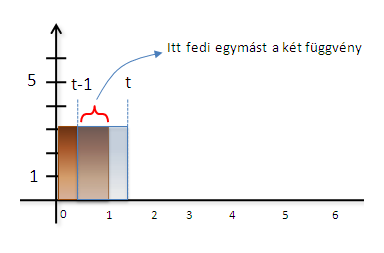
A lényeg mégegyszer: Az integrálási határok addig mennek, amíg a két függvény fedi egymást.
Ha valaki megérti ezt a mondatot, akkor utána azonnal átlátja miért kell így megválasztani az integrálban a határokat.
Végeredményben tehát ezt kaptuk: $$ (f*g)(t) = \left\{ \begin{array}{l l} 9t & \quad 0\leq t\leq1 \\ 18-9t& \quad 1\leq t\leq2 \\ 0& \quad egy\acute{e}bk\acute{e}nt \end{array} \right. $$
A következő animáció mutatja a feladatban szereplő f,g függvényeket és feketével az (f*g)-t :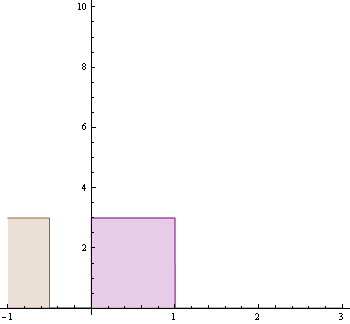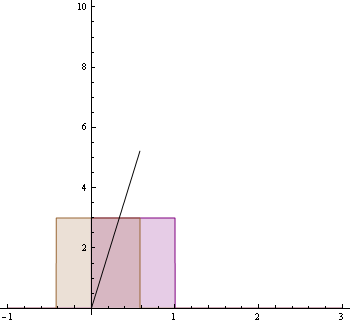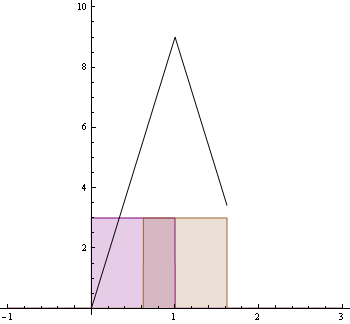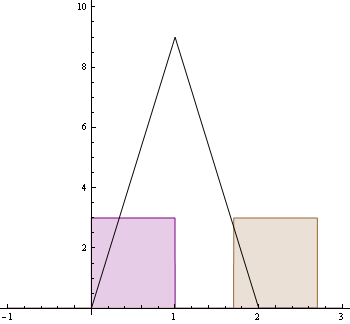 Animáció elrejtése/megjelenítése
Animáció elrejtése/megjelenítése
2.példa - Rádióaktív hulladék mennyiségének kiszámítása
Remélem ti is tudjátok, hogy így szól a rádióaktív bomlástörvény: $$ {N}(t)=N_{0}\cdot e^{-\lambda t} $$ Itt N0 a kezdeti rádioaktív atommagok száma. N(t) megmondja, hogy mennyi rádióaktív atommagunk marad még várhatóan az adott t-ben (pl. vettem N0=1mol (kb 238 gramm) uránt mennyi marad t=3nap múlva). A lambda pedig a bomlásállandó, amely megmondja, mennyi a valószinűsége, hogy egy atommag egységnyi idő alatt elbomlik. Ennek a képletnek a levezetését sok helyen megtalálhatod, pl itt is.
A feladat a következő: Van egy telep, ahová folyamatosan érkezik a rádióaktív szemét. Azt, hogy egy adott pillanatban
(t-ben) mennyi érkezik, az f(t) függvény írja le. (Figyeljétek meg: f(t) most az N0 a t-ben, azaz a kezdeti mennyiség!)
Tehát ez a rádióaktív kupac egyrészt folyamatosan nő, másrészt ezzel egyidőben
folyamatosan bomlik lefelé. A kérdés, hogy egy adott pillanatban mennyi rádóaktív anyagunk van összesen?
Namost , ha az anyagunk nem bomlana , akkor egyszerű dolgunk lenne, csak ki kéne integrálni az f(t)-t a t időpontig:
\$\displaystyle \int_{0}^{t }f(\tau )d\tau$\
(Magyarul összeadjuk az egyes időpontokban érkezett mennyiségeket.
Egyébként ha megnézitek, ez is a konvolúció egy egyszerű esete.)
Nos, mivel anyagunk folyamatosan bomlik ezért más a helyzet.
A megoldás:
1. Tegyük fel gondolatban, hogy most vagyunk t-ben. Most, f(t) mennyiségű cuccunk érkezett.
2. Tau idővel korábban
\$f(t-\tau)$\
mennyiségű cuccunk jött (ez az N0), de ebből már elbomlott mostanra valamennyi.
Ezért most ebből már csak
\$f(t-\tau) \cdot e^{-\lambda \tau}$\
van.
3. Nincs más dolgunk mint ezeket a mostanra még megmaradt rádióaktív atommagokat összegezni t-ig:
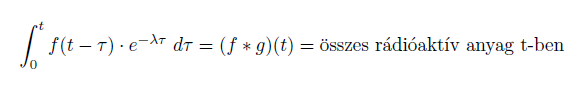
- Most fent az (f*g)-ben a g jelenti az e-lambda t függvényt -
4. Kész, remélem mindenki ráérzett a konvolúció erejére..
Ha valami nem lenne világos, akkor írjatok nyugodtan.
3.példa - csirkefarm
Talán már írtam, hogy a konvolúciót rengeteg mindenre lehet használni. Most egy olyan feladat jön, amit nem biztos, hogy elsőre konvolúció segítségével oldanánk meg.
Csirkefarmot szeretnénk üzemeltetni (képzeletföldén).
Tegyük fel hogy minden nap veszünk valamennyi kiscsirkét (0 csirkével indultunk).
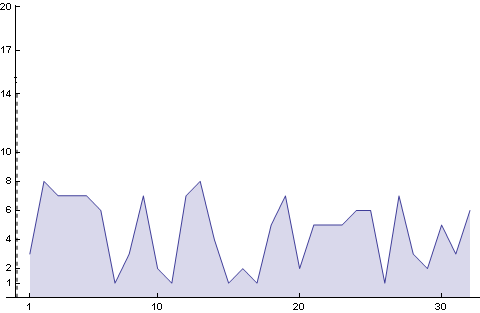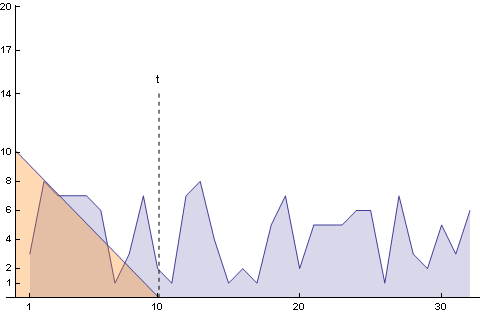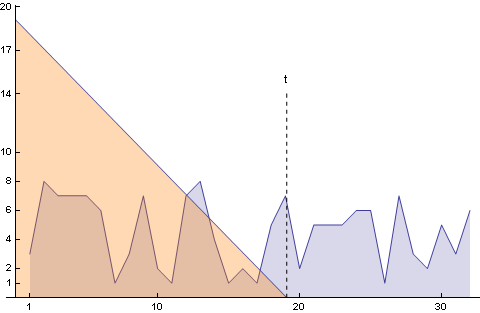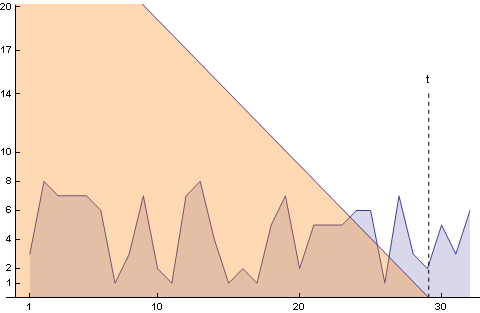
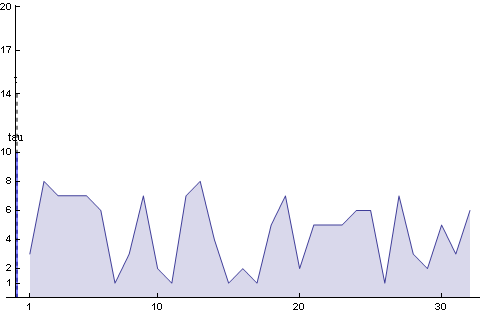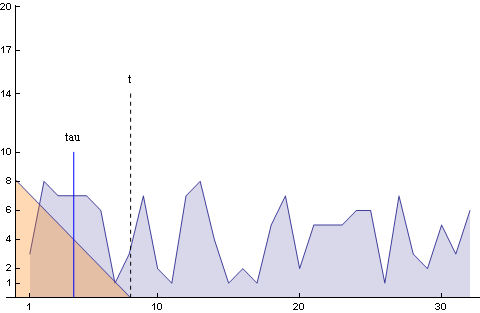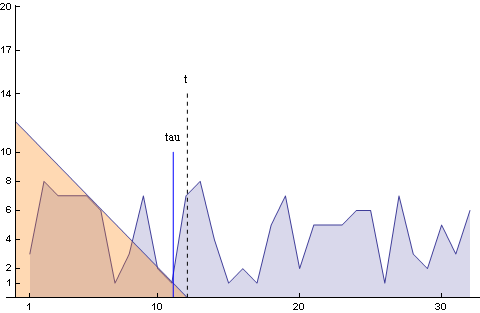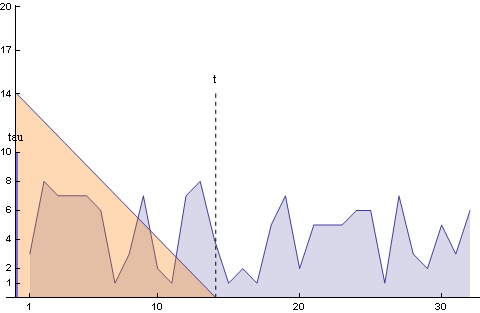
Az ábrán látható amint az 1.nap három db-ot vettünk, 2.nap nyolcat stb..
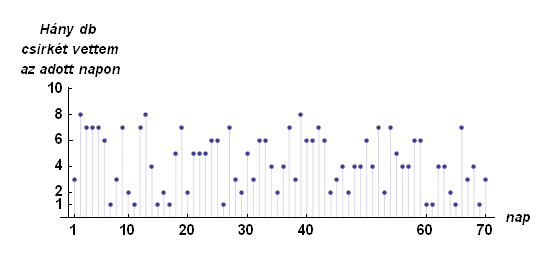 (Akik a tojásokból kikelnek, azokat a feladat során nem vesszük figyelembe )
(Akik a tojásokból kikelnek, azokat a feladat során nem vesszük figyelembe )
Ezek a csirkék, mivel folyamatosan etetjük, idővel folyamatosan nőnek.
Egyszer - pl egy hónap múlva - meg kell számolnunk hány kg csirkénk van összesen. Hogyan csináljuk?
Namost néhány feltevést kell tennünk azért, hogy a vége egyszerű legyen:
1.: Ha kiscsirkét veszünk, annak kezdeti tömege 0 kg aztán szépen
növekedik az idővel, lineárisan. Egy nap alatt 1 kg-ot. (most képzeletföldén vagyunk úgyhogy ilyeneken nem kell meglepődni..:)).
2.: A csirkék tetszőlegesen nagyra nőhetnek. (0kg-ról végtelen tömegűre.. hmm, érdemes ezt a feladatot folytatni ?)
A megoldáshoz használjuk a konvolúciót!
A fenti diszkrét függvény ami azt ábrázolta mennyi csirkét veszünk naponta legyen f(t) ! Namost én a könnyebbség kedvéért úgy kezelem
f-et mintha folytonos lenne.
A súlyfüggvény pedig legyen \$g(t) = t$\ . Azért t, mert azt mondtuk hogy minden csirke 1 nap alatt 1kg-ot hízik (1 egységnyi idő
alatt 1 "egységet" hízik folytonos esetben).
Az alábbi animáción látható az f(t) függvény, (a legelső kép, csak most folytonos, illetve csak 30 napnyi intervallumot mutat), és amint a g(t)-vel konvolváljuk. (g(t) a narancssárga) (Látható hogy t-hez képest minél távolabbi napot nézünk annál nagyobb lesz a szorzat ,- mert a korábban vett csirke nagyobbra nőtt)
 Animáció elrejtése/megjelenítése
Animáció elrejtése/megjelenítése
Mégegy: Ugyanaz az animáció látható megint, kivéve azt, hogy most ábrázoltam ahogy a tau (az integrálási változó) mozog.
(A g(t) függvény meg van fordítva ugye, ezért halad visszafelé a tau)
Ugye látható miért kell 0-tól t-ig integrálni?
Minden pontban, ahol tau áthalad összeszorozzuk f-et és g-t.
(kb 800Kb) A .gif fájl nem a legszerencsésebb animációk készítéséhez, mert túl nagyra nő a mérete, ha csak egy kicsivel részletesebb animációt csinálunk. De még mindig ezt a formátumot a legkönnyebb mozgatni/beilleszteni úgyhogy maradok ennél.
 Animáció elrejtése/megjelenítése
Animáció elrejtése/megjelenítése
Most az (f*g)(t) függvényt nem ábrázoltam, mert túl zavaros lett volna az animáció.
(f*g)(t) függvényt, vagyis hogy hány Kiló csirkénk van összesen az adott t-ben tehát a következőképp számoljuk: $$ (f*g)(t)=\int_{0}^{t} \tau \cdot f(t-\tau )\;d\tau $$Ahol g(t)=t ből most tau lett. Az f(t) függvényt már tudjuk mi: a t. napon újonan vett "csirkemennyiséget" mondja meg, de f helyére bármit tehetnénk, a feladattól függően. A fenti animációról remélem látható miért kell 0-tól t-ig integrálni, illetve az is látható , hogy most nem számoltuk bele azt hogy a csirkék egyszer elpuszulnak, sőt az sem hogy az össztömeg nem növekedhet normális esetben a végtelenségig, magyarul a g(t)-t jobban is meg lehet választani.

Zalán
Abszolút érthető, nagyon köszi a cikket!