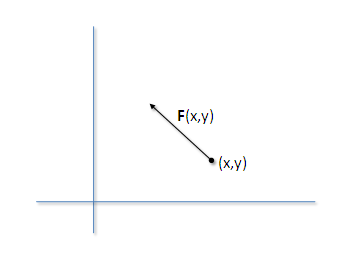
Legyen tehát F egy "vektor-vektor" függvény, \$\mathbf F: \mathbb{R}^2 \to \mathbb{R}^2$\. Ezt szemléletesen úgy lehet elképzelni, hogy minden (x,y) ponthoz a síkon hozzárendelünk egy F(x,y) vektort.
Például legyen F(x,y)=(y,-x). Számoljuk ki ezt a függvényt néhány pontban!
F(0,1) = (1,0)
F(-1,0) = (0,1)
F(0,-2) = (-2,0)
Ha ábrázoljuk a vektorokat akkor kiderül, hogy az F "forgása" az óramutató járásával ellentétes.
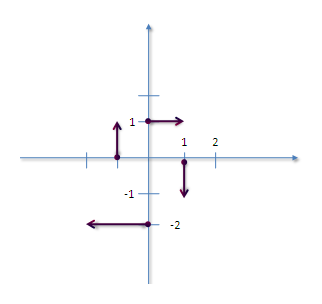
(Pl. az első esetben az (1,0) ponthoz az F(1,0) = (0,-1) = 0i -1j vektort rendeltük. Ugye a 0i -1j vektor kezdőpontja az origóban, azaz a (0,0) pontban van. Viszont képen ezt az F vektort "eltolva" ábrázoltuk, hogy a kezdőpontja az (1,0)-ban legyen. A vektor értéke ettől az eltolástól nem változott meg, csak így ábrázoljuk a vektormezőket. )
A következő ábrán már ugyanez 64 pontban látható:
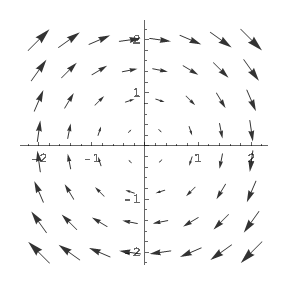
Itt egy fontos dologra fel kell hívni a figyelmet. A különböző programok mint a Matlab vagy a Mathematica, de gyakran kézzel is , úgy ábrázolják a vektormezőket, hogy azok vektorai nem eredeti méretűek, (pl az eredeti vektorok hosszának csak 30%-a), azért csinálják így, hogy az ábrák szebbek legyenek és jobban elférjenek/ne fedjék át egymást . Ez a fenti képen is látható.
Egy másik függvény, pl. G(x,y)=(x,y) képe a következő:
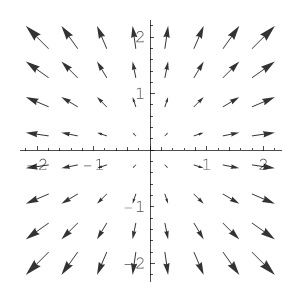
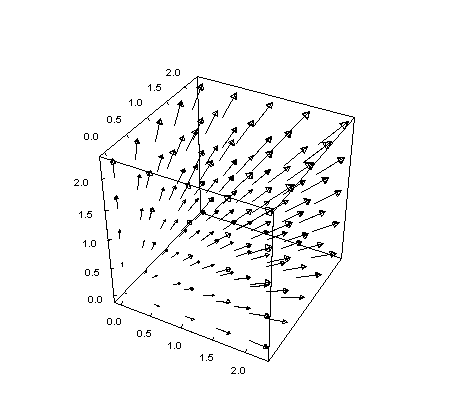
Három dimenzióban hasonlóan értelmezhetünk egy \$\mathbf F : \mathbb{R}^3 \to \mathbb{R}^3$\ vektormezőt. Most F(x,y,z)-ra gondolhatunk úgy, mint ami megadja az (x,y,z) pontban a folyadék/légáramlás sebességét. F(x,y,z) értéke tehát egy (x,y,z) kezdőpontú vektor. Ugyanez 3 dimenzióban: (most x>0 , y>0 , z>0 megszorítással)
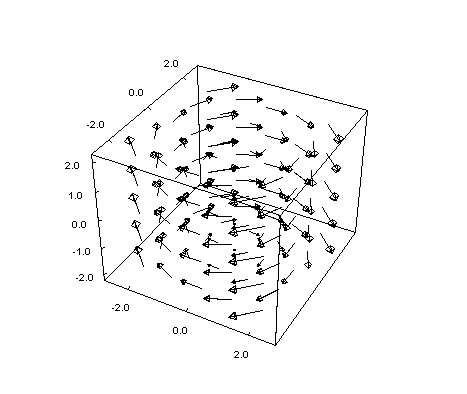
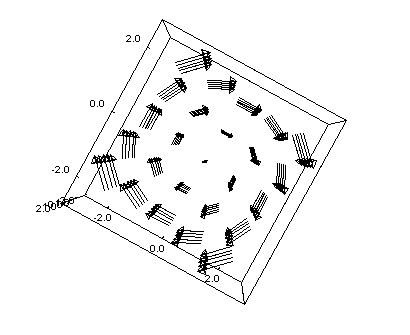
És végül a cirkuláló vektormező 3D-ben: F(x,y,z)=(y,-x,0)

Juhász Gyula
F(x,y)=(y,-x) alapján felveszem a következő pontokat:
F(1,0) = (0,-1)
F(0,-1) = (-1,0)
F(0,1) = (1,0)
F(-1,0) = (0,1)
Ha az "F vektort "eltolva" ábrázolom, hogy a kezdőpontja az (x,y)-ban legyen", akkor és egy csúcsára állított négyzetet kapok, ami az óramutató járásaval megegyező forgású. A bemutatott ábrán is megegyező irányú de talpára állított négyzet.
Jól látom?