Felület paraméterezése - példák

Két példa a felület paraméterezésével kapcsolatban:

1.példa

Írjuk le paraméteresen a feje tetjére állított kúpfelületet, amelynek egyenlete: \$z=\sqrt{x^2+y^2}$\

Megoldás: Egy fix z-re, a síkmetszet egy kör lesz, aminek a sugara z. Szóval ha pl. z=u, akkor ennek a körnek a paraméterezése:

x= u·cos v,   y= u·sin v
\$0 \leq v \leq 2\pi$\ mellett

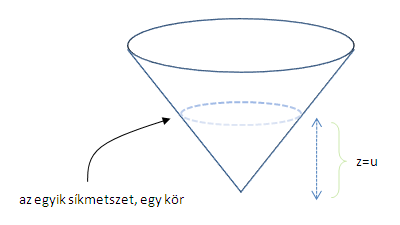
A körökből összerakott teljes felület tehát ez lesz:
$$ \Phi(u,v) = (u \cdot \cos v, \; u \cdot\sin v, \;u) $$ ahol \$0 \leq v \leq 2\pi,\; 0\leq u \leq \infty$\

2.példa

Mi történik, ha lerögzítjük a körök sugarát a következőképpen:
x = 3·cos v,
y = 3·sin v

Megoldás: A paraméterezés így alakul: $$ (x,y,z) = \Phi(u,v) = (3\cdot \cos v,\; 3\sin v, \;u) $$ Ez egy henger lesz, melynek sugara=3.