Felület paraméterezése

Mostanra már igen meghitt kapcsolatba kerülhettél a paraméteres görbékkel. Ha volt egy függvényünk \$\mathbf c[a,b] \to \mathbb{R}^3$\, akkor ezzel a \$\mathbf c(t)$\-vel egy görbét írtunk le három dimenzióban, (a t változó a-tól, b-ig megy, és ezt a t változót neveztük "paraméternek").

A paraméteres görbékről szóló cikkben többször használtam példának a \$\mathbf c(t) = (\cos t,\; \sin t,\; t)$\ függvényt, ami egy "hélixet" ír le. Itt látható \$(0 \leq t \leq 2\pi)$\ :

Java animáció megjelenítése / elrejtése (nem minden böngésző támogatja már)

A görbét tehát ily módon paramétereztük.

A felületek leírásánál is lényegében ugyanígy járunk el. Egy különbség van: a függvény most kétváltozós.

Ahhoz, hogy illusztráljuk a felületek tulajdonságait, a következő függvényt fogom használni példaként:

$$ \Phi(u,v) = (u\cdot \cos v,\; u\cdot\sin v,\; v) $$

Ha megfigyelitek, rögzített u=1 esetén \$\Phi(1,\;v)$\ az előbbi hélixet fogja kirajzolni. Ha u=0.5 ,akkor pedig \$\Phi(0.5,\;v)$\ újra hélixet fog kirajzolni, csak most feleakkora sugárral. (Az u rögzített, csak a v-t változtatjuk)

Ezután, ha u 0-tól 1-ig változhat, és v pedig 0-tól 2π-ig, akkor egy egész "hélix-sereget" kapunk.
Magyarul, így \$\Phi(u,\;v)$\ kirajzol nekünk egy felületet (egyébként a neve "csavar-felület"):

Java animáció megjelenítése / elrejtése (nem minden böngésző támogatja már)

Az animáción az alsó kék ponttal tudjuk a v-t változtatni. Ekkor a felületen lévő piros pont egy hélixet fog kirajzolni.
Az u változót a pedig zöld sliderrel változtatjuk, ilyenkor a hélix sugara változik.
Ha hagyjuk a v-t konstans értéken, akkor az u változása egy egyenes szakaszt rajzol ki.

Legyen most D egy téglalap ami a \$0 \leq u \leq 1$\ és \$0 \leq v \leq 2\pi$\ közé esik. Ekkor a \$\Phi$\ függvényre úgy tekinthetünk amely ezt a D téglalapot a fenti csavartfelület-re "képezi le". Ezt gyakran így is írjuk: \$\Phi: D \to \mathbb{R}^3$\.

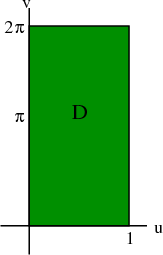
A D tehát egy téglalap az uv-síkon, aminek minden (u,v) pontját a \$\Phi(u,\;v)$\ pontra képezzük le.
Ezt világosan láthatjuk a következő képről. Ez ugyanaz mint az előző animáció volt, csak most a slidereket kicseréltük egy téglalapra.
A zöld pontot mozgatva, minden (u,v) pontpárhoz kapunk egy \$\Phi(u,\;v)$\ pontot a térben, amit a piros pont jelenít meg.

Java animáció megjelenítése / elrejtése (nem minden böngésző támogatja már)

A D-nek persze nem kell feltétlenül téglalapnak lennie. Viszont gyakran arra törekszünk, hogy D téglalap legyen, mivel így a gyakorlatban könnyebb az integrálás.

Néhány példát olvashatsz itt.