Kapcsolódó cikk:
Felületi integrál
1.példa
Legyen egy hengerfelületünk amelynek sugara 3 és magassága 5, ezt így lehet megadni :
\$x^2 + y^2 = 3^2$\ és \$0 \leq z \leq 5$\.
Ezen hengerfelület minden pontján van valamekkora töltésmennyiség (úgy is mondhatnánk, hogy a hengeren megadható
vmilyen "felületi töltéssűrűség"). Ez a töltéssűrűség arányos az xy-sík távolságával, magyarul mondva a
hengerfelület egyes "pontjainak" töltése attól függ hogy az aktuális pont milyen messze van az xy-síktól.
A feladat az, hogy számoljuk ki a teljes hengerfelület töltését.
(Figyelem, a hengernek most nincs "alja" és "teteje"!)
Megoldás: A feladatból remélem kivehető, hogy most egy valós-függvényen értelmezett felületi integrált kell majd kiszámolnunk.
A távolság egy (x,y,z) pont és az xy-sík között z, ezért a töltéssűrűség a következő függvény lesz: f(x,y,z) = kz, valamilyen k konstansra (arányossági tényező).
A teljes felület töltése pedig ezen az f-en értelmezett felületi integrál az S hengerfelületen:
\$\displaystyle \iint_S f\;dS$\.
A hengerfelületet paraméteresen így lehet felírni:
$$ \mathbf \Phi(\theta, t) = (3\; \cos \theta, 3\; \sin \theta, t) $$ ,ahol \$0 \leq \theta \leq 2\pi$\, és \$0 \leq t \leq 5$\ (a felületek paraméterezéséről itt találhatsz egy rövid leírást)A teljes felületen levő töltésmennyiség tehát:
$$ \iint_S f \; dS = \int_0^5 \int_0^{2\pi} f(\mathbf \Phi(\theta,t)) \left\|\dfrac{\partial \mathbf{\Phi} }{\partial \theta}(\theta, t) \times \dfrac{\partial \mathbf{\Phi} }{\partial t}(\theta, t) \right\| \;d\theta \;dt $$Ennek az integrálnak a részei így alakulnak:
$$ \begin{align*} f(\mathbf \Phi(\theta,t)) &= kt \\ \frac{\partial \mathbf{\Phi} }{\partial \theta}(\theta, t) &= (-3 \sin\theta, \;3\cos \theta, \;0) \\ \dfrac{\partial \mathbf{\Phi} }{\partial t}(\theta, t) &= (0,0,1) \\[8pt] \dfrac{\partial \mathbf{\Phi} }{\partial \theta}(\theta, t) \times \dfrac{\partial \mathbf{\Phi} }{\partial t}(\theta, t) &= \left | \begin{array}{ccc} \textbf{i} &\textbf{j} & \textbf{k} \\ -3 \sin \theta & 3\cos \theta & 0 \\ 0 & 0 & 1 \end{array} \right |\\[8pt] &= \mathbf i 3 \cos \theta - \mathbf j(-3\sin \theta) \\ &= (3\cos \theta, \; 3 \sin \theta, \; 0) \\ \left\|\dfrac{\partial \mathbf{\Phi} }{\partial \theta}(\theta, t) \times \dfrac{\partial \mathbf{\Phi} }{\partial t}(\theta, t) \right\| &= \sqrt{9 \cos^2 \theta + 9\sin^2 \theta} \\ &=3 \end{align*} $$Végül ezeket behelyettesítve, az eredmény: $$ \begin{align} \iint_S f \; dS &= \int_0^5 \int_0^{2\pi} kt3 \; d\theta \; dt \\ &= \int_0^5 \left( kt3\theta\bigg|_{\theta = 0}^{\theta=2\pi} \right)\;dt\\ &=\int_0^5 6\pi kt \;dt\\ &=3\pi kt^2\bigg|_0^5 = 3\pi k(25) = 75\pi k \end{align} $$
2.példa
Legyen S ugyanaz a hengerfelület, mint előbb \$x^2 + y^2 = 3^2$\ és \$0 \leq z \leq 5$\
F pedig egy vektormező: \$ \mathbf{F} (x,y,z) = (2x,\; 2y,\; 2z)$\
Számold ki az F vektormező felületi integrálját az S felületre vonatkoztatva. Használd a hengerből kifelé mutató normálvektort!
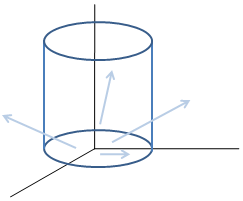 A henger és az F vektormező néhány vektora
A henger és az F vektormező néhány vektora
Megoldás: Az első kérdés, hogy mi lesz az integrál előjele? Mivel a normálvektorok és a vektormező nagyrészt egyirányba mutatnak ezért azt várjuk, hogy pozitív lesz. Ezt mindig érdemes átgondolni a feladatok előtt, mert jó lesz ellenőrzésnek.
Ahogy az első példában, most is ugyanúgy paraméterezzük a hengert:
$$ \mathbf \Phi(\theta, t) = (3\cos \theta, 3\sin \theta, t) $$ ,ahol \$0 \leq \theta \leq 2\pi$\, és \$0 \leq t \leq 5$\ Azt is kiszámoltuk, hogy: $$ \dfrac{\partial \mathbf{\Phi} }{\partial \theta}(\theta, t) \times \dfrac{\partial \mathbf{\Phi} }{\partial t}(\theta, t) = (3\cos \theta, \;3\sin\theta, \; 0) $$ A feladatban az volt, hogy használjuk a hengerből kifelé mutató normálvektort! Tehát a kérdés, hogy a \$(3\cos \theta, \;3\sin \theta,\; 0)$\ normálvektor kifelé mutat-e a felületből, avagy nem (ha gondolatban a kezdőpontját a felületre helyezzük). A válasz az, hogy igen. Itt látható amint ennek a normálvektornak a kezdőpontját a felület egy pontjába helyeztük: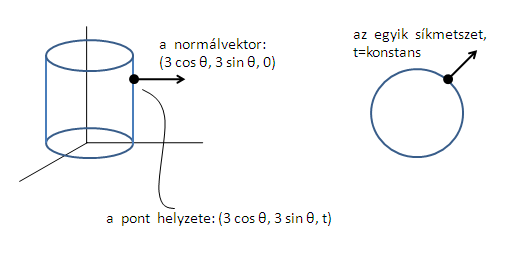
Még egy dologra térjünk ki.
Ennek a hengerfelületnek ugye kétfajta orientációja is lehetne
(a normálvektor "befelé" is mutathat), ha a normálvektort elletétesen váltasztanánk,
akkor mennyi lenne az előbb kiszámolt felületi integrál? A válasz \$-180\pi$\.
Ez remélem nem megepő ezek után.

filad
@Ákos
Köszönöm, javítva.
Akos
Üdv!
A hengerfelület paraméteres felírásakor, az intervallumok megadásánál lemaradt a \$\theta$\ mindkét példában, vagyis helyesen:
\$\mathbf \Phi(\theta, t) = (3\; \cos \theta, 3\; \sin \theta, t)$\
ahol \$0 \leq \theta \leq 2\pi $\ és\$ \;\;0 \leq t \leq 5 $\
Egyébként az oldal kiváló, nagyon tetszik hogy sok animáció és példa van az elméleti rész mellé, ami szintén érthetően van előadva. Bárcsak ilyen stílusban tanítanának egyetemen is.
Ákos