Néhány részlet a divergenciával kapcsolatban

Az előző részben arról volt szó, hogy a divergencia az egyes pontokhoz rendel egy számot, ami megmondja, hogy ott mennyi többlet-folyadék áramlik "kifelé", vagy mennyi "tűnik el" benne. De úgy is el lehet képzelni, hogy minden ponthoz rendelünk egy képzeletbeli "sűrűséget": ha több folyadék áramlik ki egy "pontból", mint amennyi bemegy, akkor annak a pontnak a sűrűsége csökken az idő függvényében, ellenkező esetben pedig nő. A divergencia ennek a kiáramló "többletnek" a mértékét adja meg. Ha a pont inkább elnyeni a folyadékot akkor ott negatív a div F(x,y,z). A vektormező persze nemcsak folyadékot reprezentálhat.

Az előző rész végén ezzel a 3 dimenziós vektormezővel fejeztük be: F(x,y,z) = xi + yj+ zj = (x,y,z) ami alul látható

Java animáció megjelenítése / elrejtése (nem minden böngésző támogatja már)

Ha kiszámoljuk a divergenciát: $$div\;\textbf{F} =\frac{\partial }{\partial x} x +\frac{\partial }{\partial y} y + \frac{\partial }{\partial z} z = 1+1+1=3$$

A divergencia mindenhol pozitív, konstans. A képről is látható, hogy a folyadék összeségéban "tágul". Ez nem meglepő, hiszen ha minden pontban pozitív a div F, akkor ez azt jelenti, hogy minden pontból több áramlik ki , mint amennyi beáramlott a másik oldalon.

A képek sokszor megtévesztőek

Ezekután nézzünk meg egy kicsivel különböző vektormezőt.

Java animáció megjelenítése / elrejtése (nem minden böngésző támogatja már) Látszólag megegyezik a fentivel, a különbség annyi, hogy a sebesség csökken az origótól távolodva. A divergenciája vajon pozitív mindenhol? Végyülis úgy tűnik igen, legalábbis ránézésre "tágul" a folyadék (egyre több és több lesz) és nem látszik, hogy lenne "nyelő"-je.
A fenti vektormező a következő: $$\mathbf{F}(x,y,z) = \frac{(x,y,z)}{(x^2 + y^2 + z^2)^{3/2}}$$ ahol (x,y,z)≠(0, 0, 0). Az előzőhöz képest annyit változott, hogy leosztottuk a origótól való távolság köbével (amit így is lehetne írni: \$\frac{\mathbf{r}}{\left \| \mathbf{r} \right \|^3}$\ , ahol r = (x,y,z) = xi + yj + zk)

Számoljuk ki a divergenciáját! $$ \def\VSpace{\Space{0pt}{0pt}{40.3px}} \begin{gather*} div \textbf{F}(x,y,z) =\frac{\partial }{\partial x} \frac{x}{(x^{2}+y^{2}+z^{2})^{3/2}} + \frac{\partial }{\partial y} \frac{y}{(x^{2}+y^{2}+z^{2})^{3/2}} + \VSpace\\ \frac{\partial }{\partial z} \frac{z}{(x^{2}+y^{2}+z^{2})^{3/2}} = \frac{(x^{2}+y^{2}+z^{2})-3x^{2}}{(x^{2}+y^{2}+z^{2})^{5/2}}+ \VSpace\\ \frac{(x^{2}+y^{2}+z^{2})-3y^{2}}{(x^{2}+y^{2}+z^{2})^{5/2}} + \frac{(x^{2}+y^{2}+z^{2})-3z^{2}}{(x^{2}+y^{2}+z^{2})^{5/2}}= \VSpace\\ = \frac{3(x^{2}+y^{2}+z^{2})-3(x^{2}+y^{2}+z^{2})}{(x^{2}+y^{2}+z^{2})^{5/2}}=0 \end{gather*} $$ Tehát ha nem vagyunk az origóban, akkor ott 0 a divergencia. A nulla divergencia azt jelenti, hogy amennyi a gömb egyik oldalán befolyt ugyanannyi ki is folyik a másik oldalon, bármelyik pontba tesszük. Úgy is mondhatnánk, hogy nem tágul a folyadék mert nincs benne "forrás" - illetve "nyelő" sem.

Hogyan egyeztethető ez össze ez a fenti képpel? Világosan látszik, hogy az origóban kell lennie divergenciának. De az a gyönyörű, hogy mégsincs, mivel az origóban nincs értelmezve a vektormező.. A képek gyakran megtévesztőek, ezért (is) van a matematika.

A divergencia dimenziótól való függése

A fenti vektormezőnél tehát ahogy telik az idő, egyik pont "sűrűsége" sem változik meg. Nincs divergecniája. Mi történik ha" átviszem" a fenti vektormezőt két dimenzióba. Azaz:

$$\mathbf{F}(x,y) = \frac{(x,y)}{(x^2 + y^2)^{3/2}}$$

,ahol (x,y)≠(0, 0). A vektormező itt látható:

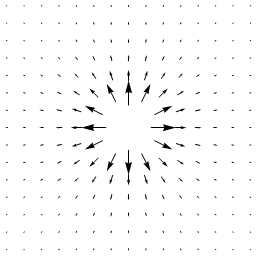
Kiszámolva a divergenciát:

$$ \def\VSpace{\Space{0pt}{0pt}{40.3px}} \begin{gather*} div \textbf{F}(x,y) =\frac{\partial }{\partial x} \frac{x}{(x^{2}+y^{2})^{3/2}} + \frac{\partial }{\partial y} \frac{y}{(x^{2}+y^{2})^{3/2}} = \VSpace\\ = \frac{(x^{2}+y^{2})-3x^{2}}{(x^{2}+y^{2})^{5/2}} + \frac{(x^{2}+y^{2})-3y^{2}}{(x^{2}+y^{2})^{5/2}}= \VSpace\\ = \frac{2(x^{2}+y^{2})-3(x^{2}+y^{2})}{(x^{2}+y^{2})^{5/2}} = \frac{-1}{(x^{2}+y^{2})^{3/2}} < 0 \end{gather*} $$

Tehát az (origón kívül) mindenhol negatív a divergencia, annak ellenére, hogy a képen olyan mintha a folyadék összességében tágulna.

Miért mutatkozik ez az eltérés a 2D és 3D között ? (Röviden: A 3D esetben a gömb felületének kevesebb mint a felén lépett be vektor (azért kevesebb mint a felén mert a vektormező "radiális" azaz egy pontból megy kifelé minden) ,és több mint a felén lépett ki belőle. A 2D esetben is radiális a vektormező, és ha beleképzelünk egy kört(az origón kívül) annak "felülete" kisebb, kevesebb a kiáramlás(a "divergálás"), és már NEM ellensúlyozza a vektormező gyors csökkenését.)

Ki lehet számolni, hogy a $$\mathbf{F}(x,y) = \frac{(x,y)}{x^2 + y^2}$$ divergenciája nulla. Viszont ha megvizsgáljuk a háromdimenziós analógját: $$\mathbf{F}(x,y,z) = \frac{(x,y,z)}{x^2 + y^2 + z^2}$$ ennek divergenciája már pozitív lesz.
Általános esetben, ha a vektormező a következőképp néz ki: $$\mathbf{F}(\mathbf{x}) = \frac{\mathbf x}{\left \| \mathbf x \right \|^p}$$ (p tetszőleges lehet),
akkor divF(x) = \$\frac{(d-p)}{\left \| \mathbf x \right \|^p}$\, ahol d azt jelenti melyik dimenzióban vagyunk.
Tehát pl 3 dimenzóban: divF(x)=(3-p)/\$\left \| \mathbf x \right \|^p$\ , ekkor tehát p=3 esetén lesz nulla a divergencia, két dimenzióban viszont p=2 esetén.