Divergencia

Ez a cikk a vektoranalízisben használt divergencia fogalmat próbálja érthetőbbé tenni.

Vektormező röviden

Legyen F egy vektor-értékű függvény, \$\mathbf{F}: \mathbb{R}^2 \rightarrow \mathbb{R}^2$\. Ekkor erre a függvényre gondolhatunk úgy, mint ami valamilyen "folyadék-áramlást" reprezentál két dimenzióban. Tehát például F(x,y) megadja a sebességet az (x,y) pontban. Ebben az esetben F -et hívhatnánk a folyadék "sebességmező"-jének is. Általánosságban F(x,y)-t vektormezőnek nevezzük. Itt találhatsz néhány példát vektormezőkre, és azok ábrázolására.

Három dimenzióban hasonlóan értelmezhetünk egy \$\mathbf{F}: \mathbb{R}^3 \rightarrow \mathbb{R}^3$\ függvényt. Most F(x,y,z)-re gondolhatunk úgy, mint ami megadja az (x,y,z) pontban a folyadék/légáramlás sebességét. F értéke tehát mindig egy vektor lesz.
F(x,y,z)-t meglepő módon háromdimenziós vektormezőnek is nevezzük.

Divergencia

Egy vektormező divergenciáját relatíve könnyű megérteni. Az alábbi F vektormező valamilyen folyadék sebességét adja meg minden pontban. Láthatóan vannak olyan pontok, ahová a folyadék csak beáramik de ki nem. Ilyen például a bal alsó sarok. Joggal mondhatjuk, hogy ezek a pontok "sűrűbbek". Vagy hogy itt a folyadék "össze-sűrűsödik".

Persze vannak olyan pontok ahová be is áramlik, de közben ki is folyik egy kicsi.
A jobb felső saroknál pedig a képről úgy tűnik, hogy a folyadék csakis kifelé áramlik.

A divergencia csak annyit csinál, hogy minden ponthoz rendel egy számot, ez a szám pedig nem más mint az ottani "sűrűség". Namost, matematikailag hogyan ragadjuk meg ezt a "sűrűséget" ?

Az előbb ezt írtam: minden ponthoz. Várjunk, egy pontnak hogyan lehet sűrűsége? Itt kap majd a határérték¹ szerepet, de ne szaladjunk ennyire előre.

Az alábbi ábrán az F(x,y) = (1/x, 0) látható. Shogy haladunk az x tengelyen felfelé, a folyadék sebessége annál kisebb lesz. A képen látható, amint egy kis zárt felületet belemerítünk ebbe a folyadékba.

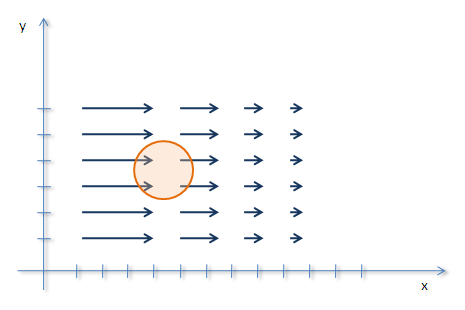
Mivel a körbe beáramló folyadék sebessége nagyobb, mint a kiáramlóé , egy adott pillanatban a belépő vízmennyiség több, mint amennyi kilép a másik oldalon. Azt is mondhatnánk, hogy a körön belül a folyadék egyre sűrűbb lesz ahogy telik az idő. Ha a kör területe a nullához tart, akkor világos hogy miért beszélhetünk "pontbeli sűrűségről". Ha ebben a vektormezőben minden pontban kiszámolnánk a ponton áthaladó folyadékmennyiséget, akkor kiderülne hogy mindehol a belépő vízmennyiség több, mint amennyi távozik. (Ezekben a pontokban negatív a divergencia, de erről majd részletesebben később.)

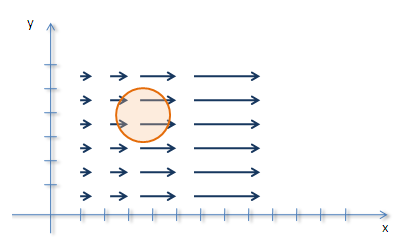
Fordítva, ha a körből kilépő vízmennyiség a több - alsó kép -, akkor a divergencia pozitív. Ezt a tulajdonságot úgy is hívjuk, hogy "forrásos". Ha egy zárt területből több folyadék jön ki mint amennyi bemegy akkor bent kell lenni valamiféle "forrásnak".

Tehát ha egy "pont" arra hajlamos, hogy onnan összességében több és több víz áramik ki akkor ott a (divF)(x,y) pozitív A "divergencia" szó is innen jön azt jelenti, hogy "széttartás", "kitágulás" stb... (De ne keverjük össze a sorozatoknál használt divergenciával.). Ha pedig a folyadék egyes pontokban sűrűsödik akkor ott mondhatnánk úgy is: "konvergál" :) (negatív a divergencia)

A divergenciát a következőképp számoljuk ki az (x,y) pontban: $$div\mathbf{F} = \frac{\partial F_x}{\partial x} + \frac{\partial F_y}{\partial y}$$ Itt F a vektormező. F_x és F_y az i,j komponenseket leíró függvények.
Ez a képlet csak annyit csinál, hogy ha mi (x,y) pontban állunk akkor itt kiszámoljuk az x tengely felöl jövő folyadék "változását" (ez egy "pontnyi" út alatt végbemenő változás, ami lehet negatív is), majd az y irányába fordulunk kiszámoljuk itt is a deriváltat, majd ezeket a különböző irányokból jövő "vízmennyiség-változásokat" összegezzük. Így megkaptuk, hogy a pont inkább "elnyeli" a vizet vagy inkább "forrásként" funkcionál. (divF -et lehetne akár (divF)(x,y) - al is jelölni. Ez egy teljen átlagos skalár-értékű függvény.)

Például vegyük a következő vektormezőt: $$\mathbf{F}(x,y) = x\mathbf{i} + y\mathbf{j}$$ tehát a komponensek függvényei: $$F_x(x,y) = x$$ $$F_y(x,y) = y$$ Ezeket deriválva majd összeadva: divF = 1 + 1 = 2. Még néhány példa itt. A divergencia most egy konstans függvény, minden pontban 2 az értéke. A F(x,y) vektormező itt látható:

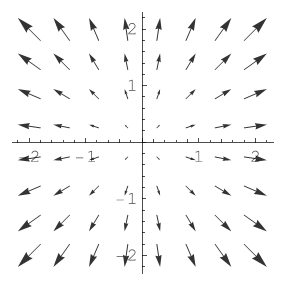A képről úgy tűnhet, hogy mintha az origóban nagyobb lenne a divergencia, de ez nem igaz. Ennél a vektormezőnél mindenhol egyforma.

A divergenciát magasabb dimenzióban is definiálhatjuk. Itt három dimenzióban látható a pozitív divergencióájú "kifelé-áramlós" kép.

Java animáció megjelenítése / elrejtése (nem minden böngésző támogatja már)

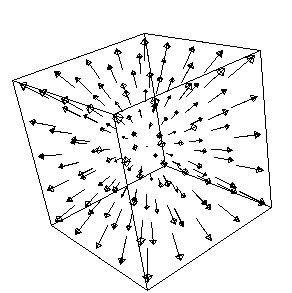
Most ugyanúgy, mint 2D-ben belerajzoltam egy kis gömböt. Talán látható, hogy - bármelyik pontba is rakjuk - több folyadék áramlik rajta ki, mint be.

Java animáció megjelenítése / elrejtése (nem minden böngésző támogatja már)

Majd a divergencia-tételnél (Gauss–Osztrogradszkij tétel) látni fogjuk, hogy a divergencia és a vektormezőben felvett zárt (pl. gömb) felületen áthaladó folyadék között közeli kapcsolat van. Ez remélem nem meglepő ezek után.

Tehát a divergencia egyike azon eszközöknek, amivel egy vektormezőt jellemezni lehet, ennyi az egész. Egy ilyen eszköz még a rotáció is.

Olvasd tovább: Néhány finomítás a divergenciával kapcsolatban. Például, hogy miért lehet megtévesztő egy kép vagy animáció ha divergenciáról van szó, illetve néhány konkrét(számolós) példa.

Egyéb kapcsolódó:
- Divergencia-tétel (avagy Gauss–Osztrogradszkij tétel)