A Green-tétel több határkomponens esetén

A bevezetőben arról volt szó, hogy a vonalintegrál (vagy cirkuláció) egy C zárt görbe mentén, egyenlő a C-n belüli ún. "mikroszkopikus cirkulációk" összegével:

$$ \int_{\partial D} \mathbf F \cdot d \mathbf s = \iint_D \left( \frac{\partial F_2}{\partial x} - \frac{\partial F_1}{\partial y} \right) \; dA $$

(A C-t gyakran \$\partial D$\-vel jelöljük, mivel a D terület határáról van szó. Erről itt van részletesebben szó. ).
A mikroszkopikus cirkulációkat zölddel álbrázoltuk a D-n:

(A C most az óramutató járásával ellentétes módon van irányítva.)
A bevezetőben bár nem hangsúlyoztam, de a D-n belül F-nek mindenhol értelmezve kell lennie.

Ez a cikk arról szól, hogy a D-nek (sárgával jelölve) nem kell mindig ilyen "szépnek" lennie. Kiderült, hogy a Green tétel olyan régiókra is alkalmazható amelyek "hézagosak".
Itt látható egy ilyen D:

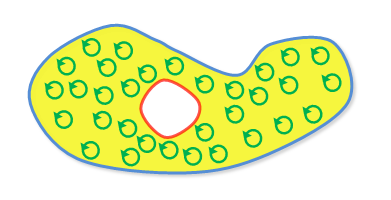
Egyértelmű, hogy most D-nek - (mégegyszer: D a sárgával szinezett területet jelenti)- két határvonala is van, az egyik a külső (kék), illetve a belső (piros).
Általában \$\partial D$\-vel jelöljük a D összes határát együttvéve, emiatt \$\partial D$\ most ugye két komponensből áll (a kék görbe, ill. a piros görbéből).

A Green tétel most is azt mondja, hogy D-n lévő "mikroszkopikus cirkulációk" összege kiadja a D határán értelmezett vonalintegrált. Viszont most a D terület határa két komponensből áll, ezért a bal oldalon lévő integrál is felbomlik két részre:

$$ \int_{C_1} \mathbf F \cdot d \mathbf s + \int_{C_2} \mathbf F \cdot d \mathbf s= \iint_D \left( \frac{\partial F_2}{\partial x} - \frac{\partial F_1}{\partial y} \right) \; dA $$

(C₁ és C₂ a kék illetve piros görbéket jelenti)
Namost a kérdés az, hogy milyen irányítást kapjanak ezek a görbék (határvonalak)?
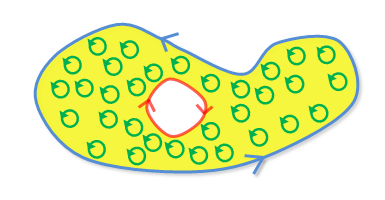
Mint már írtam a Green tétel esetében pozitív orientációjú határvonalakról beszélünk. Ez azt jelenti, hogy úgy kell irányítani a görbéket, hogy rajtuk sétálva mindig a bal oldalon legyen D terület.
A \$\partial D$\ első komponense, C₁ (kékkel), tehát az óramutató járásával ellentétes irányban halad mint az előzőekben. A C₂ viszont az óramutató járásával megegyezően.

Egyébként ha megnézed, a kék illetve piros görbék irányítása megegyezik a zöld mikroszkopikus cirkulációk irányával ott ahol "érintkeznek". (Tehát pl. látható, hogy a piros görbe alsó pontjának iránya és az ottani kis zöld cirkuláció felső részének irányítása éppen megegyezik.)

Itt már nem fogok részletesen írni róla, de ezeknél a hézagos eseteknél gyakran úgy járunk el, hogy a D területet feldaraboljuk "kezelhetőbb" részekre (amelyek már nem tartalmaznak hézagokat), és ezeken a részeken egyenként alkalmazzuk az első részből már ismert formulát.

Remélem, ezzel a két cikkel sikerült közelebb hozni, hogy a Green-tétel miképpen adja meg a kapcsolatot a rotáció és a zárt görbére vett vonalintegrál (vagyis cirkuláció) között.

Kapcsolódó cikkek:
Stokes tétel