A Stokes-tétel lényegében általánosítja a Green-tételnél már megismert gondolatokat. A rotáció, mint azt a Green-tételnél láttuk, most is nagy szerepet fog kapni, ezért azt javaslom, hogy nézz vissza ezekre a cikkekre mielőtt ezt elkezded.
A Green-tételnél röviden a következőről volt szó: Ha van egy zárt görbénk C, illetve egy két dimenziós vektormezőnk F, és ki szeretnénk számolni a C-re vett vonalintegrált ezen a vektormezőn, akkor ezt a vonalintegrált megkaphatjuk úgy is, ha összeadjuk a C-n belüli ún. "mikroszkopikus cirkulációkat".
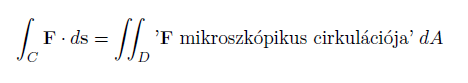
 (Ezt képet már láthattad Green-tételről szóló rövid leírásban.)
(Ezt képet már láthattad Green-tételről szóló rövid leírásban.)
Emlékezz vissza, hogy a Green tétel csak két dimenziós vektormezőknél volt érvényes, és csak olyan D tartományokra amelyek egy síkon fekszenek. A Stokes-tétel segítségével ezt három dimenzióba is kiterjeszthetjük.
Na de mit is jelent ez pontosan? Először is, a fenti ábrát képzeljük el amint egy három-dimenziós térbe helyezzük. Ekkor a görbénk, és az egész felület amit a görbével körbezárunk az xy-síkon fog elhelyezkedni.
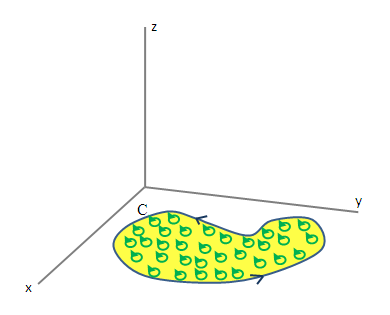
A Green tételnél láttuk, hogy a mikroszkopikus cirkulációkat (zölddel a képen) a rotáció z-komponense adta meg, azaz ekkor:
azért kellett csak a z-komponens mert ilyenkor csak az xy-síkon tartózkodunk, és mint tudjuk a rotáció egyes komponensei mindig a rájuk merőleges mikroszkopikus cirkulációt mérik.
A Stokes tétel arról fog szólni, hogy a C által körbezárt terület nem feltétlenül kell, hogy síkfelület legyen. Nézzük meg az alábbi animácót:
Java animáció megjelenítése / elrejtése (nem minden böngésző támogatja már)
A slider-t mozgatva lehet változtatni a felületet. Ezzel az animációval azt próbálom érzékeltetni, hogy a felület alakja bár változik, a "mikroszkópikus cirkulációkat" ennek ellenére lehet értelmezni a felület kicsiny darabjain, ugyanúgy ahogy a 2D-s esetben. A különbség most annyi lesz, hogy nem mindenhol a k irányú komponensét vesszük a rotációnak, hanem a normálirányút, magyarul azt amely merőleges az ottani felületdarabra:
A Stokes tétel szerint, ha összeadjuk ezeket a "mikroszkopikus cirkulációkat" a felületen, akkor megkapjuk a határoló görbére vett vonalintegrált (a görbe pirossal látható).
A Green-tételnél ugye egy sima kettős integrált kellett kiszámolnunk. Ez most megváltozik, mivel amint előbb is mondtam most a rotáció n irányú komponensére van szükségünk ami pedig minden pontban változik, ezért a kettős integrálból egy felületi integrál lesz.
Tehát a piros görbén vett vonalintegrált most egy felületi integrálból kapjuk:
(Emlékezz, a felületi integrál "összeadja" a vektormező - ami most rotF - felületre merőleges komponenseit. Ez a felületre merőleges komponens tehát most éppen az ottani mikroszkopikus cirkuláció lesz.)
A görbe persze bármilyen lehet; hajlíthatjuk, nyújthatjuk amilyenre akarjuk. Tehát a görbének sem kell az xy-síkon maradnia:
Ha jobban belegondolunk, ez a felületi integrál most egy "speciális" integrál lesz, ugyanis nem változik az értéke attól ha a felület megváltozik, magyarul független a felület "alakjától". Csakis akkor lesz más az eredmény ha a görbe (felület határa) változik. Érdekes ugye? Találtunk egy olyan felületi integrált, amely nem függ magától a felülettől!
Végül pedig azt kell megemlíteni, hogy a felület orientációjának megválasztásakor legyünk óvatosak. Ugye használhatjuk egyrészt a felületből kifelé mutató normálvektort, avagy a befelé mutatót (mivel egy felületnek általában két oldala van). A felületi integrál szempontjából nem mindegy melyiket választjuk, mert ha rossz normálvektort választunk akkor -1 szeres lesz az eredmény.
Ahhoz, hogy helyesen válasszuk meg a normálvektor irányát, most
csak egyvalamire kell emlékezni, ez pedig a
jobbkéz szabály, amit a rotációnál is láttunk.
A képen egy példa látható. Itt a normálvektor most "kifelé" mutat , de ha megváltozna a határoló görbe iránya (és ezzel együtt a mikroszkopikus cirkulációk iránya is), akkor normálvektor ellentétes lenne a jobbkéz szabály szerint.
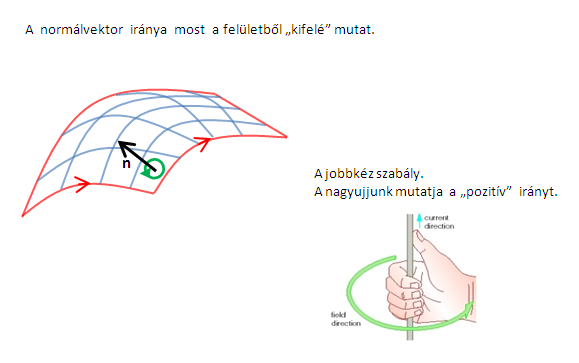
Tehát figyeljünk a normálvektor megválasztására mivel csak így lesz helyes előjelű a fenti integrál.
Néhány példa a Stokes-tétellel kapcsolatban.
Kapcsolódó cikkek:
Green-tétel
Mikroszkopikus vs. makroszkopikus cirkuláció különbség a rotáció és a "normális" cirkuláció között.
Felületi integrál
A rotáció komponensei

0 Komment