Green-tétel - példák

A példákhoz kapcsolódó cikkek:
Green-tétel
Vonaintegrál mint cirkuláció
A vonalintegrál jelölésmódjai

1.példa

Számoljuk ki a következő vonalintegrált:

$$ \oint_C y^2 \; dx + 3xy\;dy $$

,ahol C az egységkör felső fele, az óramutató járásával ellentétes irányítással:

Megoldás: A vektormező a fenti integrálból kiolvasható: \$\mathbf F(x,y) = (y^2, 3xy)$\.
A vonalintegrált most először a Green-tétellel, majd közvetlenül is kiszámoljuk (lásd alul), így összehasonlíthatjuk mennyivel nehezebb kiszámolni a hagyományos módon.

A Green-tétel tehát átkonvertálja a vonalintegrált egy kettős integrállá. Ennek a kettős integrálnak az integrandusa a következőképp alakul:

$$ \frac{\partial F_2}{\partial x} - \frac{\partial F_1}{\partial y} = 3y - 2y = y $$

A tartomány pedig amin a kettősintegrált kiszámoljuk a D lesz, azaz az egységkör felső fele (fenti kép), mivel C ezt a területet zárja körül. (Illetve, ami még fontos, hogy C irányítása most "pozitív", ha fordítva lenne akkor meg kéne szorozni a kettősintegrált -1-el, hogy a végén helyes eredényt kapjunk)

A D tartományt a következőképp írhatjuk le:

$$ -1 \leq x \leq 1,\\ 0\leq y \leq \sqrt{1-x^2} $$ A vonalintegrál tehát így alakul: $$ \begin{align*} \oint_C y^2 \; dx + 3xy\;dy &= \iint_D \left( \frac{\partial F_2}{\partial x} - \frac{\partial F_1}{\partial y} \right) \; dA\\ &= \iint_D y \;dA\\ &=\int_{-1}^1 \int_0^{\sqrt{1-x^2}} y \;dy \;dx \\ &=\int_{-1}^1 \left( \frac{y^2}{2}\bigg|_0^{\sqrt{1-x^2}}\right) \; dx\\ &=\int_{-1}^1 \frac{1-x^2}{2} \; dx \\ &=\frac{x}{2} - \frac{x^3}{6}\bigg|_{-1}^1 = \frac{2}{3} \end{align*} $$

"Hagyományos" módszer
Számoljuk ki a fenti példát, de most ne a Green-tétellel, hanem közvetlenül elvégezve a vonalintegrált.

Ebben az esetben két részre kell bontatnunk az integrált. Az első rész a képen is látható C₁ félkörvonal, a második rész pedig a C₂ egyenes szakasz.

Először számoljuk ki a C₁ mentén:
A C₁ mivel egy félkörvonal, ezért így paraméterezhetjük: \$\mathbf c(t) = (\cos t, \sin t), \quad 0\leq t \leq \pi$\.
Ennek deriváltja: \$\mathbf c'(t) = (-\sin t, \cos t)$\. A vonalintegrál tehát ezen a görbén:

$$ \begin{align*} \int_C \mathbf F \cdot d\mathbf s &= \int_0^{\pi} \mathbf F(\mathbf c(t)) \cdot \mathbf c'(t)\;dt \\ &=\int_0^{\pi} \mathbf F(\cos t, \sin t) \cdot (-\sin t, \cos t) \; dt \\ &= \int_0^{\pi} (\sin^2 t, 3 \cos t \sin t) \cdot(-\sin t, \cos t) \; dt\\ &= \int_0^{\pi} (-\sin^3 t + 3\cos^2 t \; \sin t) \; dt\\ &= \int_0^{\pi} (-\sin t(1-\cos^2t) + 3\cos^2 t \; \sin t ) \; dt\\ &= \int_0^{\pi} (-\sin t + 4 \cos^2 t\; \sin t) \;dt \end{align*} $$

Itt, az utolsó tag szinuszos része:

$$ \int_0^{\pi} -\sin t \;dt = -2 $$

a többi rész pedig (helyettesítéssel):
(legyen \$u = \cos t$\, és ezért \$du = - \sin t \;dt$\)

$$ \begin{align*} \int_0^{\pi} 4 \cos^2 t\; \sin t \;dt &= 4\cdot \int_1^{-1} -u^2 \; du\\ &= -4 \cdot \frac{u^3}{3}\bigg|_1^{-1} = -4 \cdot \left( \frac{(-1)}{3} - \frac{1}{3} = 4\cdot \frac{2}{3}\right) \end{align*} $$ A C₁ mentén tehát: $$ \int_{C_1} \mathbf F \cdot d\mathbf s = -2 + 4\frac{4}{2} = \frac{2}{3} $$

C₂ mentén pedig könnyű kiszámolni az integrált. A C₂-n végig \$y=0$\, így \$\mathbf F(x,y) = (y^2, 3xy) = (0,0)$\.
Itt tehát nulla a vonalintegrál:

$$ \int_{C_2} \mathbf F \cdot d\mathbf s =0 $$

Mindezeket összesítve:

$$ \int_{C} \mathbf F \cdot d\mathbf s = \int_{C_1} \mathbf F \cdot d\mathbf s + \int_{C_2} \mathbf F \cdot d\mathbf s = \frac{2}{3} + 0 = \frac{2}{3} $$

Ez pedig megegyezik azzal, amit előbb a Green-tétel segítségével is kiszámoltunk.

2.példa

Legyen \$\mathbf F= (y,0)$\, és D az egységkör által határolt terület. Számoljuk ki a vonalintegrált a Green-tétel segítségével.

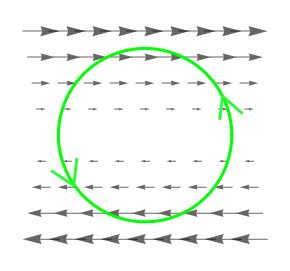
Megoldás: A vonalintegrál most negatív lesz, mivel "szemre" is úgy látszik, hogy a vektormező és a C görbe nem egy irányba haladnak (többé-kevésbé egymással szembe haladnak az egyes pontokban).

A vonalintegrál egy kettős integrálba megy át, ahogy az előzőekben is. A szükséges parciális deriváltakat kiszámolva:

$$ \frac{\partial F_2}{\partial x} = 0, \quad \frac{\partial F_1}{\partial y} = 1\\[22pt] \frac{\partial F_2}{\partial x} - \frac{\partial F_1}{\partial y} = -1 $$

A Green-tételt alkalmazva:

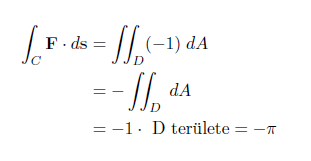Az eredmény valóban negatív, ahogy azt vártuk.