Nemcsak valós függvény vonalintegrálját tudjuk értelmezni, hanem vektormező vonalintegrálját is. Arról hogy mi a vektormező ,és hogyan lehet elképzelni egy rövid leírást találhatsz itt.
Talán mondanom sem kell, hogy ez az integrál elég fontos szerepet tölt be a többváltozós analízisen/fizikán belül.Térjünk vissza az előzőekben használt piros hélixhez, és fűzzünk fel erre a görbére egy mágnesezett fémgolyót. Ezt láthatjuk az alsó képen. Kérdezhetnéd, hogy mi az zöld téglalap a bal oldalon? Az egy nagy mágnest szimbolizál, ami mágneses mezőt hoz létre. Ez a mágneses mező zöld vektorokkal van jelölve. A mágneses mező értékét az egyes pontokban most az \$\mathbf F(x,y,z) = (-1/2, \; 0, \; 0)$\ adja meg. Ez az erő most tehát minden pontban konstans.
A piros hélixet pedig most a
\$\displaystyle \mathbf c(t) = (\cos t, \;\sin t,\; t/(3\pi)), \quad 0 \leq t \leq 6\pi$\
vektorértékű függvény adja meg .
A z-komponens azért van leosztva \$3\pi$\-vel,
hogy a hélix egy kicsit "összenyomódjon", és jobban nézzen ki.
A magenta színű fémgolyó most tehát csak ezen a görbén mozoghat.
Ha a golyó mozog akkor a vektormező munkát fog végezni (munka=F·s).
A munkát mindig az erő mozgás irányú komponenséből számoljuk.
Az alsó képeken a T jelenti a mozgás irányába mutató egységvektort, F pedig a tényleges erő irányát, ezt az F erőt "levetítve" kapjuk meg a mozgás irányába mutató erőt:
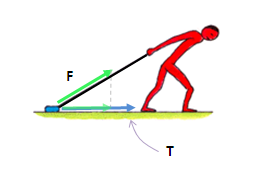
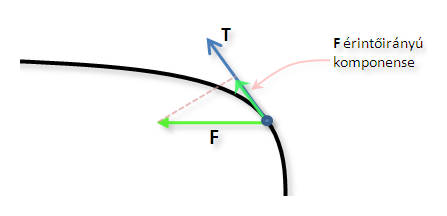 T tehát a görbe érintőirányába mutat. A kis zöld vektor az adott F erő érintőirányú komponense.
T tehát a görbe érintőirányába mutat. A kis zöld vektor az adott F erő érintőirányú komponense.
A vonalintegrál annyit csinál, hogy ezeket az érintőirányú/mozgásirányú erőket összegzi a görbe minden pontján - minden kis ds szakaszon- végigmenve. (Pontosan fogalmazva, az erők abszolút értékét összegzi, de ez gondolom egyértelmű.)
Még egy dolog hátravan: Matematikailag hogyan adjuk meg a golyó mozgásának az irányát ? Mivel a golyó egy hélixen mozog ezért ez az irány folyamatosan változik, "pontról-pontra".
Ez a pillatnyi irány, mint kiderült,
a derivált, azaz \$\mathbf c'(t)$\ (a derivált egy vektort ad meg a t pontban, ami a görbe érintőjének irányába mutat).
A \$\mathbf c'(t)$\-vel
annyi probléma van, hogy a hossza is pontról-pontra vátozik,
amit szeretnénk elkerülni.
Ezért definiáljuk a \$\mathbf T$\ "érintő egységvektort"
aminek hossza mindig egy(egységnyi) lesz, iránya viszont mindig érintőirányba fog mutatni az adott pontban:
\$\mathbf T(t) = \mathbf c'(t) / \left\| \mathbf c'(t)\right\|$\.
Mivel \$\mathbf c'(t)$\ (és ezáltal
\$\mathbf T$\ is)
érintője a görbének, ezentúl csak úgy nevezzük \$\mathbf T$\-t,
hogy érintő egységvektor. Ez a \$\mathbf T$\ alul most egy kék vektorral van
jelölve.
Amire tehát szükségünk van az az F erő érintőirányú komponense, ami nem lesz más mint a skalárszorzat:
\$\mathbf F(\mathbf c(t)) \cdot \mathbf T(t)$\
,tehát a
c(t) pontban ható F erőt (zölddel az animáción) skalárisan megszorozzuk a mozgás irányával T(t)-vel.
Röviden csak azt szoktuk írni, hogy: \$\mathbf F \cdot \mathbf T$\. Ennek a skalárszorzatnak az értéke a függőleges zöld kijelzőn látható a képen.
Érdemes feleleveníteni, hogy a skalárszorzat értéke:
- 0 ha a két vektor merőleges egymásra,
- negatív, ha a két vektor 90-től nagyobb szöget zár be,
- pozitív, ha kisebb mint 90 fokot zárnak be
Ha ezek után összeszorozzuk az erőt, ami tehát \$\mathbf F \cdot \mathbf T$\,
a megtett úttal akkor megkapjuk a munkát.
Gondolhatunk úgy \$\mathbf F \cdot \mathbf T$\-re mint egy "közönséges" skalár értékű függvényre ,ami megadja az egységnyi ds hosszra vett munkát a görbe mentén.
Ennek alapján nincs más dolgunk, mint egy valós
függvény vonalintegrálját képezni:
Ahol C a görbét jelöli. Ez az integrál lényegében összeadja a \$\mathbf F \cdot \mathbf T$\ szorzatot a görbe minden kis \$ds$\ részére.
Emlékezz vissza a vonalintegrál kiszámolására valós függvény esetében:
$$ \int_{a}^{b} f(\mathbf{c}(t)) \cdot \left \| \mathbf{c}'(t) \right \| dt $$Ha itt kicseréljük f-et \$\mathbf F \cdot \mathbf T$\-re, akkor így fog kinézni:
$$ \int_{C} \mathbf{F}\cdot \mathbf{T} \; ds= \int_{a}^{b} \mathbf{F}(\mathbf{c}(t))\cdot \mathbf{T}(t) \cdot \left \| \mathbf{c}'(t) \right \| dt $$Ez már a vektormező vonalintegrálja, de még lehet egyszerűsíteni ezen a kifejezésen. Ha visszaemlékszel arra, hogy \$\mathbf T(t) = \mathbf c'(t) / \left\| \mathbf c'(t)\right\|$\, akkor látható, hogy az abszolútértékes taggal, \$ \left\| \mathbf c'(t)\right\|$\ -vel, egyszerűsíteni lehet az integrálban. Ezért ez lesz belőle:
$$ \int_{C} \mathbf{F}\cdot \mathbf{T} \; ds=\int_{a}^{b} \mathbf{F}(\mathbf{c}(t))\cdot \mathbf{c}'(t) \; dt $$
Általában a \$\mathbf T \cdot ds$\ -et az
integrál végén \$d\mathbf s$\-el jelöljük.
Mindent egybevetve a vektormező vonalintegrálját kiszámoló végleges formula így néz ki:

filad
@snagy
Javítva, köszi.
snagy
Egy kis elírást vettem észre:
\$\displaystyle \mathbf c(t) = (\cos, \;\sin t,\; t/(3\pi)), \quad 0 \leq t \leq 6\pi $\
Itt lemaradt a koszinusznál a "t".