A vonalintegrál mint cirkuláció

Sokféle vektormező létezhet. Végtelenül sok. A matematika/fizika fejlődése során egyre nyilvánvalóbbá vált, hogy a vektormezők a gyakorlatban fontos szerepet töltenek be. Ezért természetes módon elkezdődött a vektormezők mélyebb vizsgálata, csoportosítása. Mint már írtam, a rotáció vagy divergencia is egy-egy ilyen "eszköz" a vektormezők mélyebb megértéséhez, jellemzésükhöz. És mivel végtelen sok vektormező létezik, annál jobb, minnél több eszközünk van a tanulmányozásukra..

A "mikroszkopikus vs. makroszkopikus cirkuláció" részben azt próbáltam megvilágítani, hogy a rotáció fogalma egyfajta "cirkulációt" jelent, mégpedig mikroszkopikus vagy pontbeli cirkulációt.

A "normális" cirkulációt valójában NEM a rotációval, hanem a vonalintegrállal jellemezzük. Ezt a "normális" cirkulációt úgy is nevezhetjük, hogy makroszkopikus cirkuláció.

Namost mi a fene ez a makroszkopikus cirkuláció ? , (ezt mostantól csak simán "cirkulációnak" nevezem).

A cirkuláció egy igen egyszerű dolog: a vektormezőben egy zárt görbére vett vonalintegrál értéke.
Na jó, mélyedjünk ebbe bele egy kicsit.

Emlékezz vissza, hogy a vonalintegrált: \$\displaystyle \int_C \mathbf F \cdot d\mathbf s$\ ,egy F vektormezőben és egy C görbén értelmezzük. Annyit csinált, hogy összeadta a vektormező azon komponenseit, amelyek érintőirányba mutatnak a görbén. (Alul narancssárgával látható az egyik ilyen komponensvektor. A T(t) az "érintő egységvektort" jelöli: \$\mathbf T(t) = \mathbf c'(t) / \left\| \mathbf c'(t)\right\|$\.)

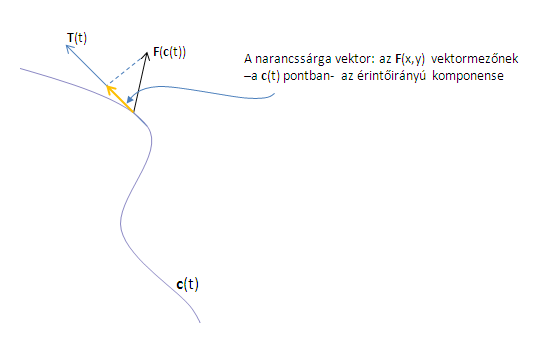
Bizonyos értelemben, a vonalintegrál azt méri, hogy a vektormező és a görbe mennyire mozognak együtt, "mennyire mennek egyirányba", az "irányítottságuk" mennyire egyezik meg. Néhány rövid példát is már írtam ezzel kapcsolatban.
Tehát, ha a egy zárt görbével van dolgunk, akkor a vonalintegrál megmondja, hogy a vektormező mennyire "cirkulál körbe" a zárt görbe mentén.
Magyarul így "leellenőrizhetjük" a vektormezőt abból a szempontból, hogy milyen erős a "forgás", vagy egyáltalán forog-e (cirkulál-e). A lényeg, hogy a görbe zárt legyen.

\$ \displaystyle \oint_C \mathbf F \cdot d\mathbf s = $\ 'F cirkulációjának mennyisége a C mentén'

Az integráljelben a zárt kör azt "hangsúlyozza", hogy zárt görbén integrálunk. Ezt néha nem teszik ki ha egyértemű, hogy az integrálás zárt görbén történik. Most én sem nem teszem ki ezek után, mert végig zárt görbén maradunk.

Érdemes szem előtt tartani, hogy a cirkuláció pozitív vagy negatív is lehet, ez C irányításától függ (a vektormező keringéséhez hasonlítva). Például, ha \$\mathbf F(x,y) = (y, -x)$\ és C pedig egy ellipszis:

$$ \frac{x^2}{4} + \frac{y^2}{9} = 1 $$

aminek az irányítása most az óramutató járásával ellentétes (ami egyúttal a vektormező forgásával is ellentétes), ezért azt várjuk, hogy az \$\displaystyle \int_C \mathbf F \cdot d\mathbf s$\ vonalintegrál negatív lesz. A görbe és a vektormező a következő ábrán látható:

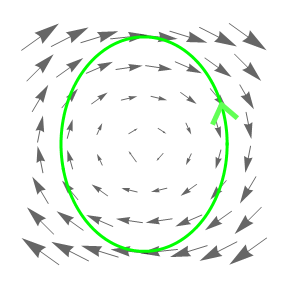Számoljuk ki a cirkulációt:
A fenti egyenletből az ellipszist paraméteres formára átírva a \$\mathbf c(t)$\ ez lesz: $$ \mathbf c(t) = (2\cos t, 3\sin t), \qquad 0\leq t \leq 2\pi $$

mivel a derivált \$\mathbf c'(t) = (-2\sin t, 3\cos t)$\, ezért a vonalintegrál így alakul:

$$ \begin{align} \oint_C \mathbf{F} \cdot d\mathbf{s} &= \int_{0}^{2\pi} \mathbf{F}(\mathbf{c}(t)) \cdot \mathbf{c}'(t) \; dt \\ &=\int_{0}^{2\pi} \mathbf{F}(2 \cos t, 3 \sin t) \cdot (-2\sin t, 3\cos t) \;dt \\ &=\int_{0}^{2\pi}(3 \sin t, -2 \cos t) \cdot (-2\sin t, 3\cos t) \;dt \\ &=\int_{0}^{2\pi} (-6\sin^2 t-6\cos^2 t) \; dt\\ &= -6\int_{0}^{2\pi} (\sin^2 t+\cos^2 t)\; dt\\ &= -6\int_{0}^{2\pi} 1\; dt = -6 \cdot 2\pi \end{align} $$

Azt kaptuk tehát, hogy egy ilyen irányú görbe mentén a vektormező "negatív cirkulációval" rendelkezik, vagy máshogy: a vektormező éppen ellentétesen "forog" mint amerre a görbe megy.

A képről nem mindig világos hogy egy vektormezőnek van-e cirkulációja vagy sem.
Az alábbi ábrán \$\mathbf F(x,y) = (-y, 0)$\, és a görbe pedig az egységkör \$\mathbf c(t) = (\cos t, \; \sin t)$\.

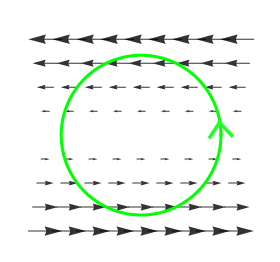
Ennél a vektormezőnél nem nyilvánvaló, hogy létezik-e "cirkulációja". Viszont ha jobban megnézed, akkor látható, hogy a vektormező és a görbe nagyrészt egy irányba halad. A "cirkuláció" valószinűleg pozitív lesz.

Számoljuk ki:

Az egységkör tehát $$ \mathbf c(t) = (\cos t, \; \sin t ), \qquad 0\leq t \leq 2\pi $$ ennek deriváltja: $$ \mathbf c'(t) = (-\sin t,\; \cos t) $$

Valamint, mivel \$\mathbf F(x,y) = (-y, 0)$\, ezért
$$ \mathbf F(\mathbf c(t)) = \mathbf F(\cos t, \; \sin t) = (-\sin t, 0) $$
A cirkuláció tehát: $$ \begin{align} \int_C \mathbf{F} \cdot d\mathbf{s} &= \int_{0}^{2\pi} \mathbf{F}(\mathbf{c}(t)) \cdot \mathbf{c}'(t) \; dt \\ &= \int_{0}^{2\pi} \mathbf{F}(\cos t, \sin t) \cdot (-\sin t, \cos t) \; dt \\ &= \int_{0}^{2\pi} (-\sin t, 0) \cdot (-\sin t, \cos t) \; dt\\ &= \int_{0}^{2\pi} \sin^2 t \; dt\\ &= \int_{0}^{2\pi} \frac{1-\cos 2t}{2} \; dt = \pi \end{align} $$

Mint látható itt is van cirkulációja a vektormezőnek (a C görbe mentén ).

Az utolsó példának van egy tanulsága. Azt mondtam előbb ,hogy a cirkuláció bizonyos értelemben a vektormező "forgását" méri. Namost miért tettem a cikk során végig idézőjelbe a "forgás" szót?
Igazság szerint, ezzel a vonalintegrállal definiált cirkuláció, nem mindig a szó szerinti "forgást" méri, hanem egy annál általánosabb tulajdonságát adja meg a vektormezőnek.
Az utolsó példánál is látszott, hogy F nem "forgott", a cirkulációja mégis pozitív volt a görbén.
Ha fizikai szemszögből közelítenénk meg, akkor a cirkuláció jelenléte annyit mondana: a C zárt görbén végigmenve, a teljes munka amit vektormező végez pozitív lesz.
Hogy miért fontos ez a zárt görbe mentén végzett "teljes munka" (vagy cirkuláció)? Vannak olyan vektormezők, ahol bármely zárt görbe mentén haladunk, a vektormező által (és ezáltal általunk is) végzett munka nulla lesz. Ezek a vektormezők, mint kiderült, különleges szerepet töltenek be a világunkban tapasztalt jelenségeknél, ezért eszméletlenül fontosak. Ezeket a vektormezőket úgy is hívjuk: konzervatív erőterek.

A cirkuláció igen nagy szerepet játszik a vektoranalízisben is. A négy alaptétel közül háromban is szerepel. Pl a Green - és Stokes tételek a cirkuláció és a rotáció közötti kapcsolatot írják le. A cirkuláció hiánya pedig, ahogy előbb is írtam, a "konzervatív" vektorterekkel áll kapcsolatban.