Paraméteres görbék és deriváltjaik

Bevezetés

Legyen c(t) egy vektor-skalár függvény két dimenzióban (\$\mathbf c: \mathbb{R} \to \mathbb{R}^2$\). Az első ábrán látható egy példa vektor-skalár függvényre. A „vektor-skalár” függvény elnevezés arra utal, hogy a függvény vektor értékű és skalár változójú. 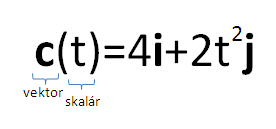Tehát pl t=1 esetre a képen a 4i + 2j helyvektort kapjuk.

Az ilyen típusú függvényekkel leírhatunk különböző görbéket a síkon, a térben, stb.. (Ahogy az egyenes paraméterezésénél is látható)

A függvény skalár változóját szokás paraméternek nevezni. (Jelen esetben a függvény "egyparaméteres".)
A paraméteres azt jelenti, hogy van egy t független változónk, és ettől a t-től függ az x és y koordináta. A t-re lehet úgy gondolni, mint pl. az időre. Ahogy haladunk az időben, úgy változik az x és y koordinátánk. (Ezt a t változót nevezzük paraméternek). Erre a paraméterezésre egyrészt azért van szükség, mert így sokkal általánosabban, illetve egyszerűbben leírhatjuk a görbéket.

Pl. 3D-ben a t-edik másodpercben a P(x(t); y(t); z(t)) pontban vagyunk. Ahol x(t) y(t) és z(t) közönséges függvények. Látható, hogy ezek a koordináta-függvények nem függnek egymástól, csakis t-től.

A lényeg tehát, hogy t minden értékéhez rendelünk egy pontot a térben, vagy a síkban.. stb.
(Matematikailag ugye valójában vektorokról van szó. Mikor azt mondom 'pont', ezt úgy is el lehet képzelni mint egy origóból induló vektor (helyvektor) végpontját. Ezért is írjuk a c(t) függvényt vastagbetűvel, mert értéke egy vektor lesz. (\$\mathbf c: \mathbb R \to \mathbb R^2$\) És ahogy haladunk a t-ben, úgy rajzolja ki a c(t) vektor végpontja a görbét. Lásd a következő videón.)

Az alsó animáción látható egy ellipszis, \$\mathbf c(t) = (3\cos t)\mathbf i + (2\sin t)\mathbf j$\. A c(t) függvény most egy kék nyíllal van jelölve.
Ahogy változtatjuk a t paramétert 0-tól 2π-ig (az alsó csúszkával), úgy rajzolja ki a vektor hegye az ellipszist.

Java animáció megjelenítése / elrejtése (nem minden böngésző támogatja már)

- Megjegyzés: Matematikailag is meg lehet mutatni, hogy ez a görbe egy ellipszist rajzol ki. Legyen \$(x,y)$\ egy tetszőleges pontja a görbének: \$(x,y) = \mathbf c(t)$\. Ekkor mivel \$\mathbf c(t) = (3\cos t, \; 2\sin t)$\ azt mondhatjuk , hogy \$x = 3\cos t$\, és \$y = 2\sin t$\. Remélem látod, hogy a következő egyenletbe miért lehet behelyettesíteni ezeket. (Ez egyébként az ellipszis egyenlete.)

$$ \frac{x^2}{3^2} + \frac{y^2}{2^2} = 1 $$

(Ha tudod , hogy \$\cos^2 t + \sin^2 t = 1$\, akkor gondolom látható, hogy \$3\cos t$\ és \$2\sin t$\ miért helyettesíthető be x és y helyére.)

A derivált értelmezése paraméterezett görbéknél

A c(t) deriváltja analóg az egyváltozós esetben használttal:

(1) $$ \mathbf c'(t) = \lim_{h \to 0} \frac{\mathbf c(t+h) - \mathbf c(t)}{h} $$

Egyváltozós esetben a deriváltat úgy értelmeztük, mint a függvény "meredekségét" az adott pontban, ott ez közönséges szám volt. Igaz-e ez egy ilyen vektorértékű függvénynél is? Most a derivált egy kicsit más: egy vektor. Mivel vektor, ezért most a deriváltnak iránya és nagysága is van.
A deriváltvektor iránya az adott pontban a görbe érintőnek irányát mutatja. Az abszolút értéke \$\left\| \mathbf c'(t) \right\|$\ pedig lényegében a "sebesség nagyságát" mondja meg az adott pontban (ha képszeletben egy részecskére gondolunk, ami a görbén halad). Itt olvashatsz erről részletesebben: Paraméteres görbék - fizikai interpretáció

Naszóval, nézzük meg hogy az (1). képlet hogyan adja meg a görbe érintőjét !
A következő animáción látható ugye a kék vektor ami c(t)-t ábrázolja. Ezen felül látható még c(t+h) zölddel, és végül a piros, ami most a deriváltvektor "közelítését" jelenti, most jelöljünk g-vel ! $$ \mathbf g(t) = \frac{\mathbf c(t+h)- \mathbf c(t)}{h} $$ (A számláló ugye a c(t)-vektorból a c(t+h)-ba mutató vektort jelenti.) A g tehát a deriválttól (1) abban különbözik, hogy nincs benne limesz.

Ha h=1, akkor g(t)=c(t+1)-c(t) , a piros vektor eleje és vége a zöld illetve a kék vektorok csúcsai lesznek. A lenti animáción látható, ha h értékét csökkented, akkor a zöld vektor egyre közelebb kerül a c(t)-hez. Így a piros vektor egyre jobban megközelíti az tényleges érintőt.
Amikor h=0, akkor a zöld és a kék vektorok ugyanazok lesznek. Határétékként pedig a piros vektor egyenlő lesz a c'(t)-vel.

Java animáció megjelenítése / elrejtése (nem minden böngésző támogatja már)

A c'(t) függvényt ezek után felhasználhatjuk pl. arra, hogy megmondjuk egy adott pontban az érintőegyenes képletét.