Paraméteres görbék - fizikai interpretáció

Már volt szó róla, hogy ha van egy c(t) függvényünk, (ami egy egyváltozós vektor-értékű függvény) akkor az ilyen függvényekre úgy lehet tekinteni, mint amik leírnak egy görbét a síkban/térben stb..

A t változóra gondolhatunk úgy mint pl. az időre, a c(t) függvényre pedig úgy, mint ami megadja a (síkbeli/térbeli..) pozíciót ebben a t időpontban.

Példának vegyük a \$\mathbf c(t) =(\cos t, \; \sin t) $\ függvényt, ahol \$0 \leq t \leq 2\pi$\.
Ez a függvény minden t-re ad egy helyvektort, amelyeknek a csúcsai az egységkör egyes pontjait rajzolják ki. Alul látható.
A c(t) függvény az egységkör egy "paraméterezése". Az igazság az, hogy egy görbét (pl. kört) sokféleképpen lehet paraméterezni.
De mit is jelent ez igazából? A cikkben ezt a kérdést járjuk egy kicsit körül.

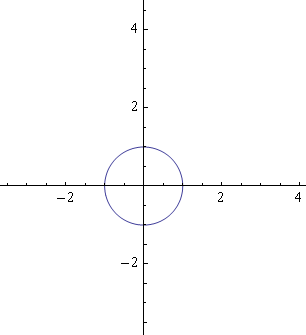Szóval, van egy c(t) függvényünk ami egy egységkört ír le paraméteresen.
Nos, ez a c(t) nem csupán magáról a körről ad információt. Máshogy mondva, egy ilyen paraméterezésből nem csak azt tudjuk meg, hogy egy kört fog kirajzolni, hanem sokkal többet:
a fenti függvény a görbe ún. "sebességéről" is ad információt!

Ha a fenti c függvény képzeletben egy részecske - vagy valami, ami körmozgást végez - mozgását írja le, akkor ez a részecske t = 2π másodperc (vagy óra, nap, hónap, vagy amilyen egységet választunk az időnek..) múlva körbeér.
A következő animáció mutatja ezt a mozgást:

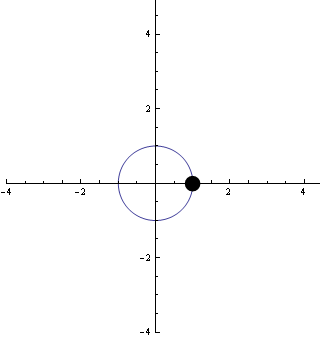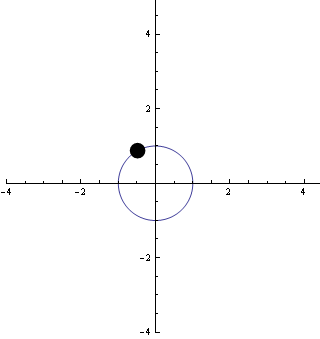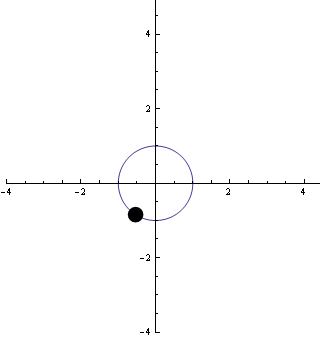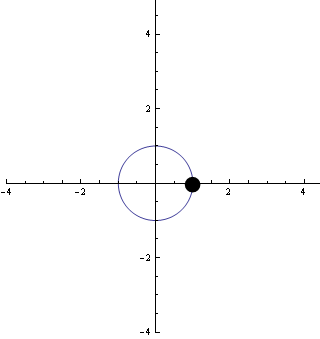
Úgy tűnik, hogy a részecske "gyorsasága" állandó, (amit matematikailag is meg lehet mutatni).
Azért nem azt mondtam, hogy a részecske sebessége, mivel a sebesség egy vektor, aminek az iránya folyamatosan változik tehát az nem állandó. A részecske "gyorsasága" alatt ennek vektornak az abszolút értékét értem.
A sebesség(vektor) az egyes pontokban ugye a derivált:

$$ \mathbf c'(t) =(-\sin t, \; \cos t) $$

, ennek a vektornak a hosszát (vagyis a részecske "gyorsaságát") pedig mindenki kiszámolhatja, hogy állandó lesz (nem függ t-től).

A következő animáció ezt a sebességvektort mutatja az egyes pontokban.

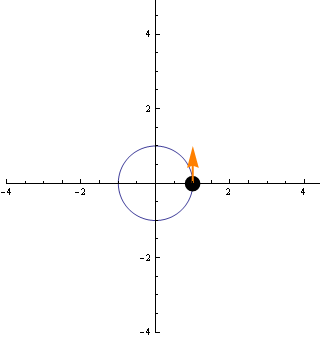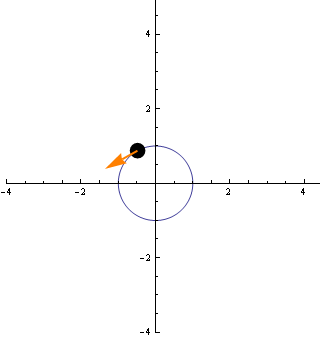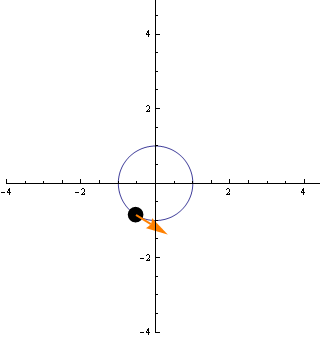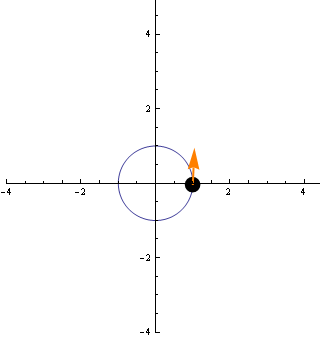Az animációról is látszik, hogy a vektor abszolútértéke állandó.

A bevezetőben azt mondtam, hogy ugyanazt a görbét többféle paramáterezéssel le lehet írni, nézzünk tehát egy másfajta paraméterezést az egységkörre:

$$ \mathbf p(t) = (\cos(t^2), \; \sin(t^2)) \qquad 0 \leq t \leq \sqrt{2 \pi} $$

A különbség annyi az előzőekhez képest, hogy most t helyett t² van.
Mégegyszer, ez a függvény ugyanazt az egységkört fogja kirajzolni! (te is megpróbálhatod vmilyen programmal ábrázolni) . Látható, hogy most a t változó 0-tól csak \$\sqrt{2\pi}$\-ig megy, (t² így fog a 0-tól \$2\pi$\-ig menni!)
Nézzük meg a mozgást amit a p-vel írhatunk le:

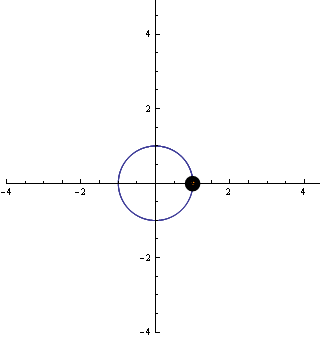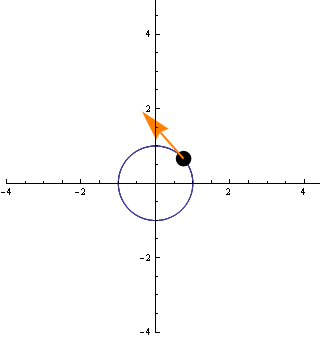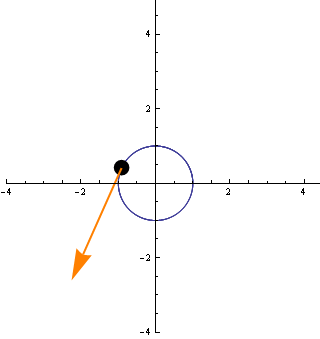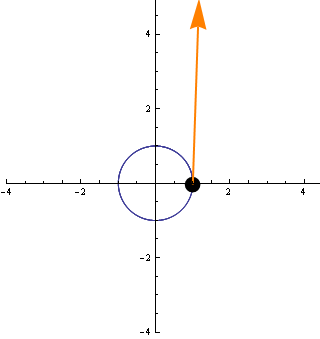
A részecske lassan elindul, majd ahogy telik az idő egyre gyorsabban mozog. Az érintővektor is ezért lesz hosszabb minden pillanatban (mégegyszer: az érintővektor - a derivált- , a részecske sebességét adja meg az egyes pontokban)

A konklúzió:
A lényeg tehát, hogy egy görbét sokféleképpen lehet paraméterezni, ezek ugyanazt a görbét rajzolják ki, viszont a görbék "sebessége" már eltértő lesz.

A konklúzió más szavakkal:
A c(t) és a p(t) tehát két eltérő ún. "paraméterezése" volt ugyanannak a körvonalnak. Ezeket az eltérő paraméterezéseket - mint látható volt- arra használhatjuk, hogy felírjuk a különbséget az ugyanazon útvonalon, de eltérő sebességgel mozgó objektumuk között.

A vonalintegrálnál kerül majd elő az, hogy mindegy milyen paraméterezést használsz, a vonalintegrál értéke nem fog változni.
A görbe ívhosszánál is írtam már erről.