Adott a következő vektormező:
$$
\mathbf F(x,y) = (y \cos x + y^2, \sin x + 2xy - 2y)
$$
A feladat az lesz, hogy találjuk meg a potenciálfüggvényét.
Először el kell döntenünk, hogy a vektormező egyáltalán konzervatív-e.
Ha kiszámoljuk a komponensfüggvények megfelelő deriváltjait:
$$
\begin{align*}
\frac{\partial F_2}{\partial x} &= \frac{\partial}{\partial x} (\sin x + 2xy - 2y) = \cos x + 2y \\
\frac{\partial F_1}{\partial y} &= \frac{\partial}{\partial y} (y \cos x + y^2) = \cos x + 2y
\end{align*}
$$
akkor láthatóan a rotáció nulla, azaz:
$$
\frac{\partial F_2}{\partial x} - \frac{\partial F_1}{\partial y} = 0
$$
Az F most az egész \$\mathbb{R}^2$\-n értelmezve van, ezért nem kell aggódnunk az esetleges komplikációk miatt, nyugodtan mondhatjuk, hogy F konzervatív.
Mivel F konzervatív ezért tudjuk, hogy létezik egy f skalár-értékű függvény melyre: \$ \mathbf F = \nabla f$\. Hogyan találjuk meg ezt az f-et, azaz a potenciálfüggvényt?
A \$\nabla f = \mathbf F$\ egyenlőség a következőt jelenti, részletesen kiírva a tagokat: $$ \left( \frac{\partial f}{\partial x}, \frac{\partial f}{\partial y} \right) = (F_1, F_2) = (y \cos x + y^2, \; \sin x + 2xy - 2y) $$ azaz, két feltételünk van:
| $$ \frac{\partial f}{\partial x}(x,y) = y \cos x + y^2 $$ | (1) |
| $$ \frac{\partial f}{\partial y} (x,y) = \sin x + 2xy -2y $$ | (2) |
Vegyük sorra ezeket a feltételeket egyenként, és nézzük meg, hogy találunk-e olyan f(x,y)-t ami mindkettőnek eleget tesz. (persze tudjuk, hogy ilyen f biztosan létezik, mivel a vektormező konzervatív.)
Kezdjük az első (1) feltétellel:
$$
\frac{\partial f}{\partial x}(x,y) = y \cos x + y^2
$$
ebben most tekintsünk úgy y-ra mintha egy egyszerű konstans lenne.
Ezekután integrálhatjuk x-szerint, ami után ezt kapjuk:
$$
f(x,y) = \int y\cos x + y^2 \;dx = y\sin x + y^2 x + C
$$
Látjuk tehát, hogy az
\$f(x,y)$\
függvény előáll az
\$y \sin x + y^2 x + C$\ alakban.
Eddig rendben is lenne, egy dolgot viszont észre kell vennünk.
A C konstans a végén mi lehet? Látható, hogy dx szerint integráltunk, és y-t konstansként kezeltük.
Ezt azt jelenti, hogy a C akár y függvénye is lehet! Tehát a végén nem C-t hanem C(y)-t kell írnunk.
A vége tehát így néz ki:
$$
y\sin x + y^2 x + C(y)
$$
Megj:
Aki esetleg még nem érti miért kell C(y) a végére:
gondoljatok bele egyváltozós fv-nél hogy nézett ki a határozatlan integrál,
pl \$\displaystyle \int x \; dx = \frac{x^2}{2} + C$\.
A C azért van benne, mert szeretnénk megadni az integrál eredményét a lehető legáltalánosabb formában.
Kétváltozóban most úgyanígy szeretnénk megmondani az
\$\displaystyle \int y \cos x + y^2 \;dx$\
integrál eredményét a lehető legáltalánosabban. Mivel most egy kétváltozós függvényt interálunk dx szerint, ezért nem csupán egy egyszerű C
konstans lehet a végén, hanem y akármilyen függvénye C(y), mivel y is konstansként kezelendő.
Megj. vége
Tehát az f(x,y) függvényünk jelenleg ilyen formát ölt:
$$
f(x,y) = y\sin x + y^2 x + C(y)
$$
ha ezt deriváljuk x szerint akkor megkapjuk az (1) feltételt, tehát a feladat felével már végeztük.
Ezután a (2) feltétellel kell foglalkoznunk.
Fogjuk a már meglévő f(x,y) függvényünket és deriváljuk y szerint:
$$
\frac{\partial f}{\partial y} = \frac{\partial}{\partial y} (y \sin x + y^2 x + C(y)) = \sin x + 2xy + \frac{\partial C(y)}{\partial y}
$$
Ha ezt összehasonlítjuk a (2) feltétellel, akkor láthatóan szerencsénk van.
Igen egyszerű dolgunk van, ugyanis a (2) feltétel teljesül, ha
$$
\frac{\partial C(y)}{\partial y} = -2y
$$
(Azt elárulom, hogy ha F nem lenne konzervatív, akkor ezen a ponton akadnánk meg,
ugyanis nem tudnák mind az (1) és (2) feltételeket teljesíteni egyszerre.)
A C(y) függvényt integrálással megkapjuk: $$ C(y) = -y^2 + k $$ ahol k konstans.
Mostmár meghatározhatjuk az f(x,y)-t. Behelyettesítve C(y) értékét, a következőt kapjuk: $$ f(x,y) = y \sin x + y^2 x - y^2 + k $$ a parciális deriváltakat kiszámolva láthatjuk, hogy ez tényleg potenciálfüggvénye F-nek, azaz $$ \nabla f = (y \cos x + y^2, \sin x + 2xy - 2y) = \mathbf F(x,y) $$
Azzal, hogy ismerjük a potenciálfüggvényt (f-et), a vonalintegrált: $$ \int_C \mathbf F \cdot d\mathbf s $$ igen egyszerű lesz lesz kiszámolni, ugyanis teljesen mindegy milyen alakú a C görbe. Az integrál értéke mindig f(q)-f(p) lesz, ahol p a görbe kezdőpontja, q pedig a végpontja.
Tegyük fel ki kell számolnunk egy vonalintegrált F-ben, ahol a C görbe a következő:
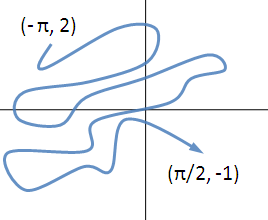A válasz egyszerűen:
$$
\begin{align*}
\int_C\mathbf F \cdot d\mathbf s &= f(\pi / 2 , -1) - f(-\pi, 2 )\\
&=-\sin \pi/2 + \frac{\pi}{2} -1 + k - (2\sin(-\pi)-4\pi-4+k)\\
&= - \sin \pi/2 + \frac{9\pi}{2} + 3 = \frac{9\pi}{2}+2
\end{align*}
$$
(a k konstans egyébként mindig ki fog esni belőle)
Megj: Ha esetleg valamilyen feladatban egy komplikált görbét kapsz, akkor az egy jó jel, hogy F konzervatív vektormező.
Fanatic
Szia!
Ezt értem, de hogyan csináljuk 3D-s vektortérben? Nekünk az is lehet a ZH-ban. Előre is köszi.