Konzervatív vektormezőkben nincs cirkuláció

Ha egy F vektormező konzervatív (vagy útfüggetlen), akkor a vonalintegrál $$ \int_C \mathbf F \cdot d\mathbf s $$ nem függ az aktuális C görbétől; a vonalintegrál értéke csak a kezdőponttól (nevezzük p-nek) és a végponttól (q) függ. Nézzük meg mi következik ebből a definícióból.

Tegyük fel hogy van két tetszőleges görbénk C₁ és C₂. Mindkettő p-ből q-ba halad. 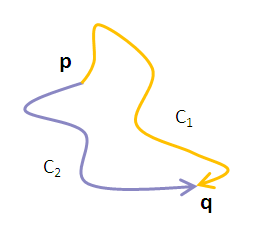Mivel tudjuk hogy F "útfüggetlen", ezért a két vonalintegrál megegyezik: $$ \int_{C_1} \mathbf F \cdot d\mathbf s = \int_{C_2} \mathbf F \cdot d\mathbf s $$

Mi lenne, ha megfordítanánk a C₂ irányát, úgy hogy q-ban kezdődjön és p-ben végződjön? Ennek az új görbének legyen a neve C₂^―. Mivel az új görbe bármely pontján az érintővektor éppen ellentétes lesz az eredetivel, így $$ \int_{C_2^-} \mathbf F \cdot d\mathbf s = -\int_{C_2} \mathbf F \cdot d\mathbf s $$ ,magyarul ha megfordítjuk C₂-t akkor a vonalintegrál a -1 szeresére változik.

Ezekután tekinthetünk úgy erre a két görbére mintha egy C zárt görbe két "darabja" lenne: 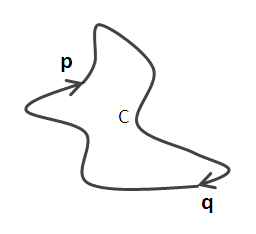(remélem látható, hogy most C nek nevezzük a fenti C₁ és C₂^― uniójából kapott zárt görbét)

A C görbére vett vonalintegrál pedig egyszerűen a két rész összege. Ennek értéke pedig 0, ugyanis C₁ -en és a C₂^― -n a vonalintegrálok éppen egymás ellentétei: $$ \int_{C_2^-} \mathbf F \cdot d\mathbf s = -\int_{C_1} \mathbf F \cdot d\mathbf s $$ A C-n tehát: $$ \int_C \mathbf F \cdot d\mathbf s = \int_{C_1} \mathbf F \cdot d\mathbf s + \int_{C_2^-} \mathbf F \cdot d\mathbf s $$

Már volt róla szó, hogy ha C egy zárt görbe, akkor a $$ \int_C \mathbf F \cdot d\mathbf s $$ vonalintegrált "cirkulációnak" is nevezzük. A cirkuláció bizonyos értelemben azt méri, hogy a görbe mentén "mennyire forog körbe" a vektormező.

A lényeg a fent elmondottakból: ha F egy konzervatív vektormező, akkor a cirkuláció bármely zárt görbe mentén nulla. (ez egyébként fordítva is igaz)
Ha csak egyetlen olyan zárt C görbét találunk ahol $$ \int_C \mathbf F \cdot d\mathbf s \neq 0 $$ akkor már tudjuk hogy F nem konzervatív , azaz "útfüggő".

Node miért fontos ez az egész, amit eddig elmondtam?
A konzervatív vektormezőket úgy definiáltuk, hogy bennük "a vonalintegrál két pont között - bármely görbén is haladunk - mindig megegyezik".
Mostantól ezt úgy is megfogalmazhatjuk, hogy "bármely zárt görbe mentén a vonalinterál nulla".

A zárt görbék pedig azért lesznek fontosak nekünk, mert sok mindennel kapcsolatban vannak. Emlékszünk még a Green- és Stokes tételekre? Igen, ők azok akik a cirkuláció és a rotáció közti kapcsolatot adják meg.
Ahhoz, hogy egy vektormezőről megmondjuk konzervatív-e ki kéne számolnunk a vonalintegrált bármely két pont között levő minden lehetséges görbén, és meg kéne mutatnunk hogy ezek mindig megegyeznek. Ezt így közvetlenül nem tudjuk megoldani.
Most viszont látjuk, hogy elég lenne megmutatni, hogy minden zárt görbén nulla-e a vonalintegrál. A következő részben látni fogjuk, hogy ez már megoldható. Érdekes módon, végtelen sok zárt görbét már jobban tudunk kezelni, mint végelen sok nem zártat.

Kapcsolódó cikkek:
Green-tétel
Stokes-tétel
A rotáció