Területszámítás és a Green tétel

Az előzőekben arról volt szó, hogy a Green tétel segítségével más módon is kiszámolhatjuk az \$\displaystyle \oint \mathbf F \cdot d\mathbf s$\ vonalintegrált.

Ha 2 dimenzióban vagyunk, C egy egyszerű zárt görbe, és F(x,y) mindenhol értelmezve van C-n belül, akkor használhatjuk a Green tételt, ami átalakítja a vonalintegrálunkat egy kettős integrállá.
Tehát az \$\displaystyle \oint \mathbf F \cdot d\mathbf s$\ helyett elég csak a következő kettős integrált kiszámolni: $$ \iint_D \left( \frac{\partial F_2}{\partial x} - \frac{\partial F_1}{\partial y} \right) \; dA $$

A kérdés, hogy lehet-e ezt az egészet fordítottan alkalmazni? Magyarul, ha adva van egy kettős integrál, akkor használhatjuk-e a Green tételt, hogy "visszaalakítsuk" egy vonalintegrállá, majd így számoljuk ki? Ez a kérdés jogos, mivel vannak olyan esetek, amikor egy kettős integrált is nehéz kiszámolni, talán így vonalintegrállá alakítva lehet, hogy éppen egyszerűbb lenne.
Másrészt, csak simán matematikailag is érdekes kérdés, hogy meg lehet-e fordítani.

A válasz az, hogy igen. Viszont vannak bizonyos megkötések.

Ha van egy kettős integrálunk $$ \iint_D f(x,y) \; dA $$ csak akkor használhatjuk a Green tételt "visszafelé", ha f(x,y) előállítható egy F(x,y) vektormezőből a következőképp: $$ f(x,y) = \frac{\partial F_2}{\partial x} - \frac{\partial F_1}{\partial y} $$ , ahol \$F_1, \quad F_2$\ a komponensfüggvények.
Jó, jó, de mégis honnan tudjuk, hogy az f(x,y) felírható-e így, található-e ilyen F vektormező hozzá, és ha található akkor pontosan mi az F?
Erről most nem fogok itt részletesen írni, de van egy egyszerű és érdekes eset.

Ha van egy D tartományunk, akkor ennek a területe ugye következő:

D területe = \$\displaystyle \iint_D 1 \;dA = \iint_D \;dA$\

,tehát ilyenkor az f(x,y) = 1 függvényt kell integrálni a megadott D-n. Ebben az esetben viszont nagyon könnyű megfelelő F vektormezőt találni !
Azaz, most könnyen mutatható olyan F melyre igaz, hogy: $$ \frac{\partial F_2}{\partial x} - \frac{\partial F_1}{\partial y} = f(x,y) = 1 $$ Rengeteg ilyen vektormező van ami kielégíti ezt az egyenlőséget, mi most az \$\mathbf F(x,y) = (-y/2, \; x/2)$\ -t választjuk.
(Levezetheted, hogy tényleg \$\displaystyle \frac{\partial F_2}{\partial x} - \frac{\partial F_1}{\partial y} = 1$\ )

Végül, összegezve a leírtakat:
Ha C egy az óramutató járásával ellentétes írányítású, egyszerű zárt görbe, ami ugye körbezár vmilyen tartományt (jelöljük D-vel), akkor ennek a D-nek a területét a következő vonalintegrállal is ki lehet számolni:

D területe = \$\displaystyle \int_C \mathbf F \cdot d\mathbf s = \frac{1}{2} \int_C x\; dy -y \; dx $\

, ahol \$\mathbf F(x,y) = (-y/2, \; x/2)$\
(Ha a fenti jelölésmód nem lenne ismerős, akkor a vonalintegrál jelölésmódjai részben van róla néhány szó)

Így lehet tehát a Green tételt "fordítva" használni.
Szerintem nézzünk egy példát.

Példa

Számoljuk ki az \$ x^2 + y^2 \leq 4$\ egyenlőtlenséggel megadott D körlap a területét a Green tétel segítségével.

Megoldás: Most persze tudjuk különösebb számolás nélkül is, hogy ez egy \$ r=2$\ sugarú kör, melynek a területe \$4\pi$\, ez jó lesz majd ellenőrzésnek.

A kört (D határát) így paraméterezhetjük:
$$ \mathbf c(t) = (2 \cos t, \; 2\sin t), \quad 0 \leq t \leq 2\pi $$
ennek deriváltja,
$$ \mathbf c'(t) = (-2\sin t, \; 2 \cos t) $$

és a Green tétel szerint tehát:

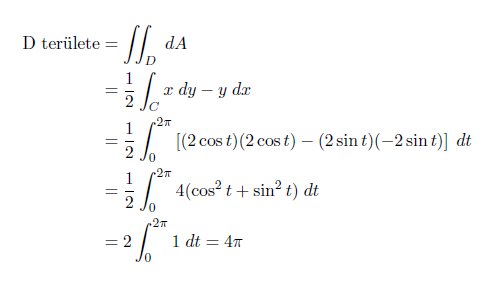
Az eredmény 4π, ami valóban a fenti körlap területe.

Kapcsolódó cikk:
Vonalintegrál példák