Vektormező vonalintegrálja - példák

Példák vektormező vonalintegráljával kapcsolatban.

1. példa

Az egyes pontokban ható erőt most az F(x,y) = (0,x) függvény adja meg. Tehát ahogy haladunk felfelé az x-tengelyen, az y-irányba mutató komponens egyre nagyobb lesz.

Számítsuk ki az erőtér által végzett munkát, amint egy részecske halad keresztül rajta a képen látható zöld C görbén. (Ez a görbe most egy egységkör, ami az első negyedben van értelmezve.)

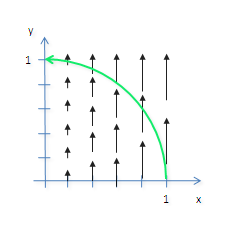
Megoldás: Előszöris látod-e, hogy a vonalintegrál most miért lesz pozitív?
Észrevehető, hogy a vektormező és a görbe "szemre" egy irányba haladnak: a görbe is felfelé tart , és a vektormező is.
Ha odaképzeled a görbe érintőjét, akkor az mindig 90 foknál kisebb szöget zár be a vektormező vektorjaival. Ezért a skalárszorzatuk mindenhol pozitív lesz.

A megoldáshoz először meg kell adnunk a c(t) görbét. A feladat alapján ez most: $$ \mathbf c(t) = (\cos t, \; \sin t), \qquad 0\leq t \leq \frac{\pi}{2} $$ de másfajta paraméterezés is nyugodtan lehetne.

Így $$ \mathbf F(\mathbf c(t)) = (0, \; \cos t) $$ és $$ \mathbf c'(t) = (-\sin t, \; \cos t) $$

A vonalintegrál tehát a következőképp alakul:

$$ \begin{align} \int_{C} \mathbf{F} \; d\mathbf{s}&=\int_{a}^{b} \mathbf{F}(\mathbf{c}(t))\cdot \mathbf{c}'(t) \; dt \\ &=\int_{0}^{\pi/2} (0,\cos t) \cdot (-\sin t, \cos t ) \;dt \\ &= \int_{0}^{\pi/2} \cos^2 t \; dt\\ &= \int_{0}^{\pi/2} \frac{1+\cos 2t}{2} \;dt\\ &=\frac{1}{2}\left( t+\frac{\sin 2t}{2}\right) \bigg|_{0}^{\pi/2} \\ &= \frac{1}{2} \cdot \frac{\pi}{2} = \frac{\pi}{4} \end{align} $$

1b. példa

Az integrál \$\displaystyle \int_C \mathbf F \cdot d\mathbf s$\ nem függ a paraméterezéstől, (ha a C görbe iránya sem változik). Ahhoz hogy ezt lássuk a gyakorlatban is, vegyük az 1. példában látható görbét, csak egy másik paraméterezéssel:

$$ \mathbf{p}(t)= (\sqrt{1-t^2},t) \qquad 0\leq t\leq 1 $$ Tehát ez a p(t) függvény most ugyanazt a negyedkörívet rajzolja ki (ha ezt nem hiszed el, akkor próbáld meg kirajzolni valamilyen programmal!)
Számoljuk ki erre is a mező munkáját!

A p deriváltja: $$ \mathbf{p}'(t)=\left( \frac{-t}{\sqrt{1-t^2}}\;,1\right) $$ A munka pedig: $$ \begin{align} \int_{C} \mathbf{F} \; d\mathbf{s}&=\int_{0}^{1} \mathbf{F}(\mathbf{p}(t))\cdot \mathbf{p}'(t) \; dt \\ &=\int_{0}^{1} \mathbf{F}(\sqrt{1-t^2},t) \cdot \left( \frac{-t}{\sqrt{1-t^2}}\;,1\right) \;dt\\ &=\int_{0}^{1} (0,\sqrt{1-t^2}) \cdot \left( \frac{-t}{\sqrt{1-t^2}}\;,1\right) \;dt\\ &=\int_{0}^{1} \sqrt{1-t^2} \;dt \end{align} $$

Most alkalmazhatjuk a \$t = \sin(u)$\ helyettesítést, ekkor \$dt = \cos(u) du$\. Mivel a \$t$\ \$0$\-tól \$1$\-ig ment, ezért az \$u$\ most \$0$\-tól \$\pi/2$\-ig megy.
Az integrál tehát a következő lesz:

$$ \begin{align} \int_{C} \mathbf{F} \; d\mathbf{s}&=\int_{0}^{1} \sqrt{1-t^2} \;dt\\ &=\int_{0}^{\pi/2} \sqrt{1-\sin^2u} \cdot \cos u\;du\\ &=\int_{0}^{\pi/2} \sqrt{\cos^2u} \cdot \cos u\;du\\ &= \int_{0}^{\pi/2} \cos^2 u \; du \end{align} $$ Ha jobban megnézed, ez éppen az 1. példában szerepelt (a 3.sorban), csak az \$u$\ helyén \$t$\ volt. Ennek az értéke (azaz a munka) ugyanannyi mint előbb: \$\pi /4$\.

2. példa

A vonalintegrál értéke általában függ attól, hogy milyen alakú görbén haladunk. Az 1.példában az (1,0) pontból mentünk a (0,1) pontba egy negyedköríven, de mehettünk volna egy másik útvonalon is, nézzünk egy példát: 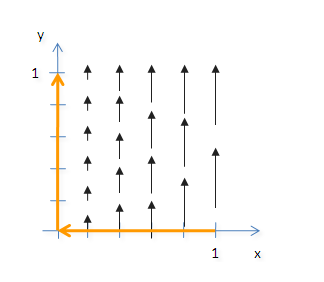A kérdés, hogy most mennyi az \$\displaystyle \int_C \mathbf F \cdot d\mathbf s$\ ?
(Az F vektormező ugyanaz mint az előzőekben.)

Megoldás: A megoldáshoz, most nem kell semmilyen számolást végeznünk.
Az út első felében, mikor az x-tengelyen balra haladunk, a görbe merőleges az erővonalakra, így ezen a részen nulla a mező által végzett munka. Az út második felében, mikor felfelé haladunk szintén nem végzünk munkát, mivel ott az F vektormező értéke nulla. Ezért,

$$ \int_C \mathbf F \cdot d\mathbf s = 0 $$

Látható volt tehát , hogy az F vektormezőben ha különböző utakon haladunk két pont között, akkor más és más munkát kell végeznünk. Ha az egyik úton haladunk, akkor lehet hogy elég sok munkát kell végeznünk, míg ha egy kicsit változtatunk az útvonalon, akkor lehet, hogy munkát sem kell végeznünk!

A vektormezők vizsgálata során kiderült, hogy vannak teljesen másfajta vektormezők is. Lehet, hogy furcsának tűnik elsőre, de olyan vektormező is létezhet, amelyben mindegy milyen úton haladunk két pont között mindig ugyanannyi munkát fogunk végezni. A lényeg csak az, hogy a kezdőpont és a végpont ugyanaz legyen, az út "alakja" nem számít.
Mint kiderült, ezeknek a vektormezőknek igen különös tulajdonságaik vannak. Az egyik az, hogy nagyon szoros kapcsolatban állnak a világunkban tapasztalt jelenségekkel. Hogy miért, az érdekes kérdés, talán majd egy másik részben én is írok róla.