A rotáció komponenseinek levezetése

A cikk első felében röviden átismétlem a rotációval kapcsolatos dolgokat. A második felében pedig a rotáció a z-irányú komponensének levezetéséről lesz szó. Minden komponenst lényegében ugyanígy kell levezetni, ezért mutatom csak a z-irányút.

***

A rotáció ugye egy vektor volt minden pontban. Ezt a vektort fel lehet bontani i,j és k irányú komponensekre. Példaként a képen látható egy (a,b) pontban a rotáció z-irányú komponense - \$(\mbox{rot} \mathbf F) \cdot \mathbf k$\ -.

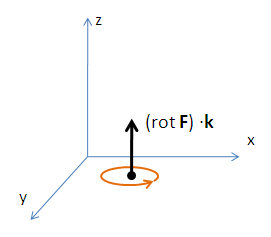
Namost, ennek a z-komponensnek nagysága megadta az ún. "mikroszkopikus cirkulációt" a z-tengelyre merőleges síkon az (a,b) pont körül. (ez most a képen az xy-sík)

Ez a "mikroszkopikus cirkuláció" szemléletesen egy nagyon kicsi zárt görbén értelmezett vonalintegrál. Úgy kapjuk meg, hogy fogunk egy zárt vonalinterált és ennek értékét leosztjuk a körbezárt területtel - a terület határértékben a nullához tart; lásd a levezetést. Ezért is nevezzük ezt gyakran területegységre eső cirkulációnak.
A képen is végtelenül kicsinek kell elképzeni a narancssárga zárt görbét.

A rotáció komponenseinek vizsgálatakor láttuk, hogy a z-komponens ez volt: $$ \frac{\partial F_2}{\partial x}(a,b) - \frac{\partial F_1}{\partial y} (a,b) $$
Ez tehát a mikroszkopikus cirkuláció mennyisége a z-iránnyal merőleges síkon, az (a,b) pont körül, és ezt a képletet fogjuk levezetni a továbbiakban. (Látható, hogy csak az F₁ és F₂ komonensfvek szerepelnek benne. Az F₃, a harmadik komponens, ami z-irányú, viszont NEM. A z-irányú komponens nem játszhat bele az xy síkon levő cirkulációba.. )

***

Z-komponens levezetése:

Az F(x,y) most tehát végig egy két dimenziós vektormezőt jelöl.

A cirkuláció egy zárt görbe mentén a következő: $$ \oint_C \mathbf F \cdot d\mathbf s $$ (A továbbiaban, a "cirkuláció" mindig egy zárt görbére vett vonalintegrált jelent.-> A vonalintegrál mint "cirkuláció")

A "területegységre eső cirkuláció" tehát: 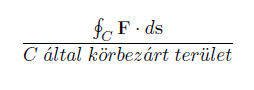Ha a C görbe egyre kisebb lesz, és pontszerűvé válik, a fenti törtből a már említett kifejezés lesz: 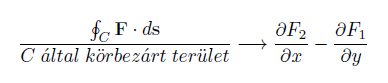A továbbiakban ezt a határértéket vezetjük le.

Legyen a C egy téglalap alakú zárt görbe. A görbe irányítása az óramutató járásával ellentétes. A C görbét a bal alsó pontban jelöljük (a,b)-vel, továbbá a szélessége legyen \$\Delta x$\, a magassága pedig \$\Delta y$\. Az oldalakat jelöljük rendre C₁, C₂, C₃, C₄ -el. 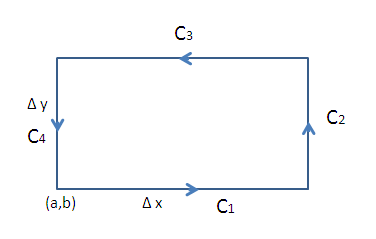A téglalap mivel elég kicsi, feltehetjük hogy az oldalai mentén konstans értéket vesz fel.

Tehát \$C_1$\ mentén a görbe \$y$\ változója konstans \$b$\ értéket vesz fel. Az \$x$\ változó viszont \$a$\-tól \$a + \Delta x$\ -ig változna. De mivel most feltettük, hogy a téglalap elég kicsi, tehát az \$[a, \; a+\Delta x]$\ intervallumban konstans értéket vesz fel a függvény, ezért a \$C_1$\ mentén \$\mathbf F(x,y)$\-t mindenhol közelíthetjük \$\mathbf F(a,b)$\-vel

A \$C_2$\ oldal mentén az \$x$\ váltazó konstans, az \$y$\ változó pedig \$ [b, \; b+ \Delta y]$\ között változik. Mivel a téglalap kicsi ezért feltehetjük azt, hasonlóan az előzőhöz, hogy \$\mathbf F(x,y)$\ értéke míg \$b$\ -ből \$b+\Delta y$\ -ba megy konstans marad. Ez a konstans legyen most \$b$\. Tehát \$\mathbf F(x,y)$\ értékét a \$C_2$\ mentén \$\mathbf F(a+\Delta x, \; b)$\-vel közelítjük. (Az \$a + \Delta x$\ változó végig konstans marad, mert most a \$C_2$\ "görbén" csak az \$y$\ mentén mozgunk.)

Ugyanígy, a \$C_3$\ mentén az \$y$\ konstans \$b+\Delta y$\ értéket vesz fel. Az \$x$\ viszont "\$a$\" és "\$a + \Delta x$\" között változik. Így \$\mathbf F(x,y)$\-t a \$C_3$\ -on \$\mathbf F(a,\; b+\Delta y)$\-al közelítjük

Végül \$C_4$\ mentén az \$y$\-t konstans \$b$\-nek vesszük (annk ellenére, hogy \$b$\ és \$b+\Delta y$\ között válozik). Tehát \$\mathbf F(x,y)$\ értékét \$\mathbf F(a,b)$\ -nek vesszük a \$C_4$\ oldalon.

Az alsó képen összegezve vannak \$\mathbf F(x,y)$\ értékei a görbe egyes oldalai mentén:

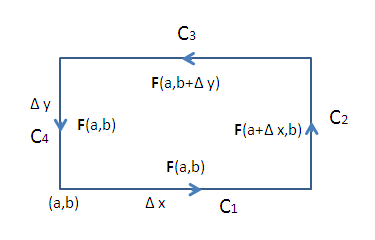
Egy rövid vonalintegrálról szóló cikkben már írtam róla, hogy ha ki akarjuk számolni a \$\displaystyle \oint_C \mathbf F \cdot d \mathbf s$\ vonalintegrált, akkor ez ugyanaz mintha az \$\mathbf F \cdot \mathbf T$\ skalárfüggvényt integrálnánk a \$C$\ görbén, ahol \$\mathbf T$\ az adott pontban a "derivált egységvektor". (Azért vektor, mert paraméteres görbék deriváltja már nem skalár, hanem egy vektor az adott pontban.) $$ \oint_C \mathbf F \cdot d \mathbf s = \oint_C \mathbf F \cdot \mathbf T\; ds $$

Ki kell tehát számolnunk \$\mathbf F \cdot \mathbf T$\ értékét a \$C$\ minden szegmensére (minden oldalára). A \$\mathbf T$\ tangens vektor minden szegmensen konstans, így az \$\mathbf F \cdot \mathbf T$\ skaláris szorzat is minden C szegmens esetén konstans lesz. Számoljuk ki ezeket a \$\mathbf F \cdot \mathbf T$\-ket:

\$C_1$\ mentén a görbe a pozitív \$x$\ irányba mutat, tehát a derivált egységvektor: \$\mathbf T =(1,0)$\. A skalárszorzat \$\mathbf F \cdot \mathbf T$\, pedig egyszerűen az \$\mathbf F(x,y)$\ első komponense lesz: $$ \mathbf F \cdot \mathbf T = F_1(a,b) $$

\$C_2$\ mentén a görbe irányítása a pozitív \$y$\ irányba esik. A derivált egységvektor: \$\mathbf T = (0,1)$\. A skalárszorzat \$\mathbf F \cdot \mathbf T$\, pedig az \$\mathbf F(a+\Delta x,\; y)$\ második komponense lesz: $$ \mathbf F \cdot \mathbf T = F_2(a+\Delta x, \; b) $$

\$C_3$\ esetén a görbe a negatív \$x$\ irányba mutat: \$\mathbf T=(-1,\; 0)$\ . Ezért a skalárszorzat \$\mathbf F \cdot \mathbf T$\, pedig az \$F_1(a,\;b+\Delta y)$\ második komponense (-1 szer) : $$ \mathbf F \cdot \mathbf T = -F_1(a,\;b+\Delta y) $$

\$C_4$\ mentén a görbe a negatív \$y$\ irányba mutat. \$\mathbf T=(0,-1)$\, tehát \$\mathbf F \cdot \mathbf T$\ egyenlő az \$F(a,b)$\ második komponensével, szorozva minusz 1-el: $$ \mathbf F \cdot \mathbf T = -F_2(a,b) $$

Az alábbi ábrán összegezzük mindezt:

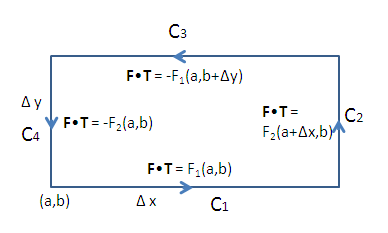
Az integrálokat mostmár könnyű kiszámítani az egyes oldalak mentén. Minden \$C_k$\ mentén mivel az \$\mathbf F \cdot \mathbf T$\ konstans, ezért csak össze kell szorozni az adott oldal hosszával:

\$C_1$\-en \$\mathbf F \cdot \mathbf T$\ értéke végig \$F_1(a,b)$\. \$C_1$\ hossza pedig \$\Delta x$\, ezért:

$$ \oint_{C_1} \mathbf F \cdot d\mathbf s = \oint_{C_1} \mathbf F \cdot \mathbf T = \oint_{C_1} F_1(a,b)ds = F_1(a,b)\Delta x $$

\$C_2$\ mentén az integrál \$F_2(a+\Delta x,\; b)$\ szorova az oldal hosszával, \$\Delta y$\-nal:

$$ \oint_{C_2} \mathbf F \cdot d\mathbf s = F_2(a+ \Delta x , \; b) \Delta y $$

\$C_3$\-ra és \$C_4$\-re pedig ezeket kapjuk:

$$ \oint_{C_3} \mathbf F \cdot d\mathbf s = -F_1(a, \;b+\Delta y) \Delta x \\ \oint_{C_4} \mathbf F \cdot d\mathbf s = -F_2(a,b) \Delta y $$

Az integrál mostmár az egész \$C$\ mentén egyszerűen a fenti tagok összege:

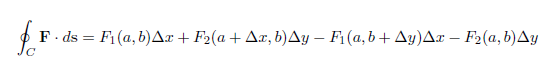
A területegységre eső cirkuláció egyszerűen csak a fenti integrál osztva a téglalap területével, \$\Delta x \Delta y$\ -al:

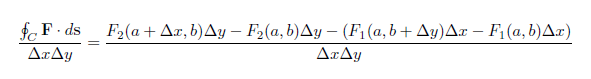
, ahol a számlálóban átrendeztem a tagokat. Majd két részre bontva a törtet, \$\Delta y$\-nal, majd \$\Delta x$\-el egyszerűsíteni lehet:

Az első részt egyszerűsítve \$\Delta y$\-nal: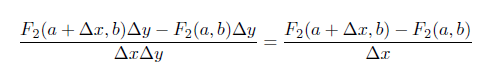
Majd a tört második részét \$\Delta x$\-el:

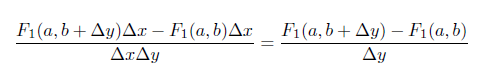
Az egész együtt tehát:

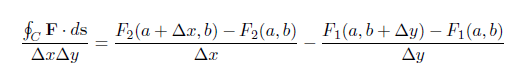
Ahogy a C görbe 0-hoz tart így \$\Delta x\to 0$\ és \$\Delta y \to 0$\. Így a fenti két tört, a jólismert dologhoz tart: \$\mathbf F$\ parciális deriváltjaihoz.

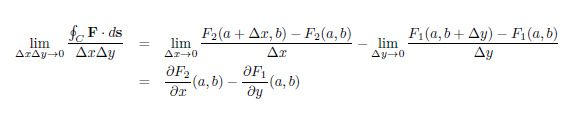
Ezzel tehát megmutattuk, hogy a területegységre eső cirkuláció az (a,b) pont körül következő: (nevezhetnénk "mikroszkopikus cirkulációnak" is) $$ \frac{\partial F_2}{\partial x}(a,b) - \frac{\partial F_1}{\partial y}(a,b) $$ Ez pedig a rotáció egyik komponense. A rotáció többi kompoensének kiszámítását is ugyanígy kell elvégezni, csak a különböző síkokban.

Megjegyzés:
A Green tételnél látjuk majd azt, hogy ha egy C vel körbezárt felületen ki akarjuk számolni a C vonalintegrálját, akkor lényegében csak a ezeket a felületen belüli, kis "pontbeli" cirkulációkat kell összeadni(integrálni), és ezután megkapjuk a teljes C-re a vonalintegrált: $$ \iint_D \left(\frac{\partial F_2}{\partial x}(a,b) - \frac{\partial F_1}{\partial y}(a,b)\right) \; dA = \oint_{\partial D} \mathbf F \cdot d\mathbf s $$ ahol \$C = \partial D$\, az óramutatóval ellentétes irányítású görbe amin vonalintegrálni szeretnénk (és ami a \$D$\ felületet körbezárja).