Néhány cikk a példákhoz kapcsolódóan:
Divergencia
A rotácó
A rotáció komponensei
Néhány kiegészítés a rotáció komponenseivel kapcsolatban
A rotáció komponenseinek levezetése
Egy egyszerű példa jön divergencia és rotáció kiszámolására. Mivel itt lényegében csak deriválni kell, ezért mutatok csak egy példát. A gyakorlatban a rotációt és a divergenciát leginkább a fizikában használjuk (fizikai jelenségek tömör leírsára/jellemzésére). A rotációt használjuk még a Stokes-tételnél , a divergenciát pedig a Gauss-tételnél. Most ezekről itt nem fogok írni.
Már az előzőekben volt róla szó, hogy a következőképp számoljuk ki őket: $$ \begin{align} & div \textbf{F}=\frac{\partial F_1}{\partial x}+\frac{\partial F_2}{\partial y}+\frac{\partial F_3}{\partial z} \\ & \\ &rot \textbf{F} =\left(\frac{\partial F_3 }{\partial y} - \frac{\partial F_2}{\partial z},\quad\frac{\partial F_1 }{\partial z} - \frac{\partial F_3}{\partial x},\quad\frac{\partial F_2 }{\partial x} - \frac{\partial F_1}{\partial y}\right) \end{align} $$ ahol F1, az F vektormező első komponensfüggvénye, F2 a másiodik komponensfüggvénye stb..
1.példa Számoljuk ki az F=(-y,xy,z) vektormező divergenciáját és rotációját.
Mivel:
$$ \frac{\partial F_1}{\partial x}=0 ,\; \frac{\partial F_2}{\partial y}=x ,\; \frac{\partial F_3}{\partial z}=1 $$ ezért a divergencia divF = 0+x+1 = x+1.
A rotációja pedig, a komponenseket deriválva:
$$
\frac{\partial F_1}{\partial y}=-1 ,\;
\frac{\partial F_2}{\partial x}=y
$$
$$
\frac{\partial F_1}{\partial z}=\frac{\partial F_2}{\partial z}=\frac{\partial F_3}{\partial x}=\frac{\partial F_3}{\partial y}=0
$$
,ezért a rotáció rotF= (0-0,0-0,y+1) = (0,0,y+1)
Az F=(-y,xy,z) vektormező képe alul látható, (nem hiszem, hogy bárki ki tudná találni csupán a képről van-e a vektormezőnek divergenciája, és/vagy rotációja, még jó hogy itt van a matematika, amivel nemcsak azt tudjuk megmondani, hogy van vagy nincs divergencia, de pontosan ki is tudjuk számolni..)
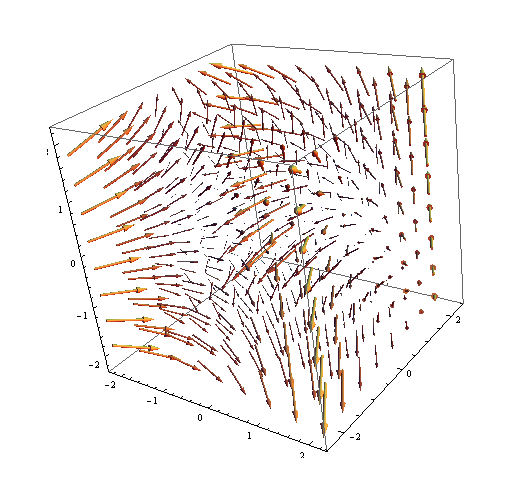

meres5
OK.
Ha ráddobnak egy atombombát, az nagyrészt divergencia.
Ha elkap egy tornádó, az többnyire rotáció...
Remélem sikerült megvilágítani :-)
M5
ketteske
Ez szuper alap fizika zh-ra! Köszi szépen, hasznos oldal :)
Nézelődő
Mármint gimnáziumban nem tanítanak rotációt, divergenciát.
Zsolti
Nézelődő
'Azt hittem hogy olyan magyarázat lesz ezekre a fogalmakra, amit egy általános iskolás is megérthet'.
Ha rotációról, divergenciáról van szó, akkor egy jóval erősebb alapszintű matek tudásra van szükséged, mint egy általános iskolai. Melyik általánosban deriválnak? Mivel a rotáció és a divergencia deriválást igényel... Tudtommal pl még gimnáziumban sem.
Ez a cikk szerintem arra jó, ha felsőoktatási területen tanulja valaki (mint pl én is), akkor egy szemléletesebb, más oldalról megközelített magyarázatot ad az olvasónak, mint az ottani előadáson. Ennél könnyebb út nincs a megértéshez. Itt nem lehet egyből a lecsóba csapni.
Mégis hogyan vezetnél az úton autót, ha nem tudod, melyik a gázpedál, és mit kell vele csinálni?
Zsolti
kérdező
Elolvastam a div és rot cikkeket is, de nekem ez kínai. Oké, még ezt a krix-krax matematikát sem értem, meg az R2-re azt hittem hogy valós számok a négyzeten :) szóval ez szerintem abszolút matematikusi vénát kíván hogy megértsék. Azt hittem hogy olyan magyarázat lesz ezekre a fogalmakra, amit egy általános iskolás is megérthet, de ezek a pontok sűrűségei meg stb. már ott megdőlnek hogy mi adta az okot hogy ilyenen valaki is elkezdjen gondolkozni, mikor aztán feltalálták???
Azzal egyetértek, hogy pl. egy folyótorkolatnál egy gát tervezésénél fontos lehet hogy milyen erős áramlás fog eróziót stb. okozni és mélyíteni a medret, rongálni a védművet, de mikor a zárt körről beszélünk a példában, abba hogy lép folyadék, mikor zárt? Szóval ezek logikai bukfencek, miközben a megértést akarnák segíteni!
Ha mondjuk a fizikában a mágneses vagy elektrosztatikus térről beszélünk, ahol én elősször fejeltem e fogalmakkal, akkor egy mágnesrúd végein vizsgált pólusok esetén mondhatjuk hogy divergenciája, azaz széttartása vagy sűrűsödése van az erővonalaknak, ha pl. vasreszelékkel szemléltetjük és egyben rotációja is a rúd két végén és a mágnesben párhuzamosan futó erővonalaknak pedig csak divergenciája van, de nincs rotációja, elhajlása?