A rotáció fogalma egy fokkal bonyolultabb , mint a divergenciáé. (Itt most egy vektormező rotációjára gondolok, - annak aki eltévedt volna.) Röviden, a rotáció egy folyadék (vagy vektormező) egy "speciális" forgását jellemzi, amit úgy is nevezhetnénk, hogy a folyadék mikroszkopikus cirkulációja. Hamarosan kivilágosodik minden, higgyétek el :-)
Képzeld el, hogy az \$\mathbf F : \mathbb{R}^3 \to \mathbb{R}^3$\ vektormező az alábbi animáción, valamely folyadék áramlását ábrázolja (de lehet levegő is, pl. egy hurrikán). Láthatóan a folyadék körben kering, az óramutató járásával ellentétes módon.
Helyezzünk egy kis labdát (vagy gömböt) ebbe a folyadékba, és rögzítsük le ennek a gömbnek a középpontját. Azért fontos ez, hogy a gömb ne tudjon a folyadék forgása miatt elmozdulni a helyéről. Másrészt viszont azt megengedjük, hogy gömb egyhelyben tudjon forogni a saját középpontja körül. Ez a gömb látható alul. A vektormező rotációja egy vektor az adott pontban - most az origóban -, ennek a vektornak a hossza a gömb forgásának sebességével egyenlő. (A gömbnek valójában végtelenül kicsinek kell lennie, mert emlékezz: a rotáció a mikroszkopikus forgást méri -erről az egészről majd részletesebben később)
Tehát a vektormező - F - meghatározza hogy egyrészt milyen irányba, másrészt hogy milyen gyorsan pörög a kis gömb. Definíció szerint F vektormező rotációja - amit rot F-el jelölünk - maga is egy vektor, aminek az iránya a gömb forgástengelyével párhuzamos, hossza pedig a gömb pörgésének "gyorsaságával" egyezik meg (az adott pontban).
Rajzoljuk le ezt a vektort az origóban! Előszöris a hossza ugye egyenlő a kis gömb forgásának sebességével. Az iránya a forgástengellyel párhuzamos, de ! ,hogy pontosan megmondjuk, definiálnunk kell hogy melyik legyen a negatív és melyik a pozitív irány. Megegyezés szerint a rotációnál az un. "jobbkéz szabály"-nak megfelelően választjuk meg, hogy merre mutasson a vektor.
A jobbkéz szabály: hajlítsd be a jobb kezeden az ujjaidat, kivéve a nagyot. Ha az ujjaid a kis gömb forgásával megegyező irányába mutatnak, akkor a nagyujjad mutatja a rot F vektor irányát.
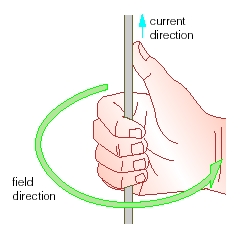A rot F vektor az origóban tehát itt látható:
Ki lehet számolni, hogy ennél a vektormezőnél a rot F értéke minden pontban ugyanannyi. (Bár a legtöbb vektormezőre ez nem jellemző.) Tehát például a kis gömböt egy másik pontba helyezzük, akkor ugyanolyan "irányban" és ugyanolyan sebességgel fog forogni. Ha a lenti animációt nézed, ki is lehet találni hogy miért.
(Kivehető amint a középponttól távolodva a vektorok egyre hosszabbak lesznek, és a gömb egyik felére az áramlás nagyobb erőt fejt ki mint a másikra. Bár a vektormező értéke ahogy haladunk távolabb egyre nő, de a gömbre ható erők aránya (és iránya) mindig ugyanolyan marad. Így tehát bárhova tesszük, a gömb mindig ugyanabba az irányba forog, és ugyanolyan sebességgel, bár az utóbbi nem látható a képről egyértelműen, de kiszámolható.)
Ezzel még közel sincs vége. Olvasd tovább : A rotáció komponensei.
Egyéb cikkek:
- Mikroszkopikus vs. makroszkopikus cirkuláció
különbség a rotáció és a "normális" cirkuláció között.
-Illetve: Néhány példa a rotációval és divergenciával kapcsolatban.
0 Komment