Görbe ívhossza - példák

Néhány példa görbe ívhosszának kiszámolására:

1. példa

Írjuk fel az (1,2,3) pontban kezdődő és a (3,1,2)-ben végződő egyenes(szakasz) egyenletét. Ezután számoljuk ki ennek a szakasznak a hosszát.

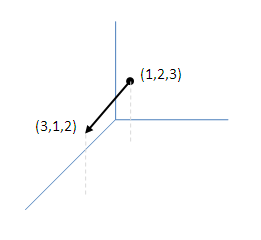
Megoldás: A vektor ami \$(1,2,3)$\-ból \$(3,1,2)$\-be mutat: \$\mathbf d = (3,1,2)-(1,2,3) = (2,-1,-1)$\. Ezután már felírhatjuk a szakaszt (az egyenes paramáterezése példákhoz hasonlóan):

$$ \mathbf c(t) = (2,-1,-1)t + (1,2,3) \qquad 0\leq t \leq 1 $$

A szakasz hosszának kiszámolásához:

$$ \mathbf c'(t) = (2,-1,-1) \qquad 0\leq t \leq 1 $$ $$ \left\| \mathbf c'(t) \right\| = \sqrt{2^2 + (-1)^2 + (-1)^2} = \sqrt{6} $$ Eztután behelyettesítve ezeket, a vonalintegrál értéke:

$$ \int_a^b \left\| \mathbf c'(t) \right\| \;dt = \int_0^1 \sqrt{6} \;dt = \sqrt{6} $$

Igazság szerint, a gyakorlatban értelmetlen egy egyenes szakasz hosszát ily módon kiszámolni. Ilyenkor elég csak a \$\mathbf d$\ vektor (képen látható) abszolút értékét kiszámolni, és meg is kaptuk a szakasz hosszát. Úgyhogy most ezt csak a példa kedvéért számoltam integrállal.

2. példa

Most nézzük az 1.példában levő görbe egy másfajta paraméterezését! $$ \mathbf p(t) = (2,-1,-1)(e^t -1) + (1,2,3) \qquad 0\leq t \leq ln\;2 $$

Feladat: Számítsuk ki a görbe hosszát.

Most a \$\mathbf p(t)$\ ugyanazt az egyenes szakaszt írja le, mint az előbb volt!
Meg lehet figyelni, hogy \$(e^t -1)$\ egyenlő nulla, ha \$t=0$\, illetve \$1$\, ha \$t=ln\;2$\. Ha most \$\mathbf p(t)$\ egy részecske mozgását írná le, akkor egy egyenes szakaszon menne \$(1,2,3)$\-tól \$(3,1,2)$\-ig, ahogy \$t$\ \$0$\-tól \$ln\; 2$\-ig változik. A különbség csak annyi az 1.példához képest, hogy most nem mozogna konstans sebességgel.
(Néhány sort már írtam erről: Ugyanazon a görbén, de különböző sebességgel mozgó részecskék)

Megoldás: Használjuk újra a görbe ívhosszánál levezetett képletet.

$$ \mathbf p'(t) = e^t(2,-1,-1) $$ $$ \left\| \mathbf p'(t) \right\| = e^t \left\| (2,-1,-1) \right\| = e^t \sqrt{6} $$

Az ívhossz tehát: $$ \int_a^b \left\| \mathbf p'(t) \right\| \; dt = \int_0^{ln2} e^t \sqrt{6} \;dt = \sqrt{6}(e^{ln2} - e^0) = \sqrt{6} $$

Az 1. és 2. példa tehát egy fontos dologra hívja fel a figyelmet: A görbe ívhossza nem függ a paraméterezésétől.

3. példa

Számoljuk ki a következő hélix ívhosszát: \$\mathbf c(t) = (\cos t, \sin t, t) \quad 0 \leq t \leq 6\pi$\.

A derivált:

$$ \mathbf c'(t) = (-\sin(t), \cos(t), 1) $$
,ennek abszolútértéke: $$ \left\| \mathbf c'(t) \right\| = \sqrt{\sin^2(t)+ \cos^2(t)+1} = \sqrt{2} $$ A ívhossz tehát: $$ \int_0^{6\pi} \sqrt{2} \; dt = \sqrt{2} t\bigg|_0^{6\pi} = 6\pi\sqrt{2} $$