Útfüggetlen, avagy konzervatív vektormezők

Kezdjük ott, hogy miért konzervatív. Ez a kifejezés a fizikából jön, az angol nyelvben a megmaradási törvényeket általánosságban "conservation laws"-nak nevezik. És éppen erről van szó, a konzervatív vektormezőkkel egy bizonyos energiafajta megmaradását tudjuk jól leírni/jellemezni. Hogy ez a fizika szemszögéből mit jelent, arról írtam pár sort kiegészítésként amit itt találhatsz.

Azt, hogy egy vektormező konzervatív a következőképp fogalmazzuk meg: a vektormezőben egy testet mozgatva a-ból b pontba, a végzett munka nem függ az út alakjától amelyen az a-ból b-be haladunk.
Emiatt gyakran nevezzük ezeket a vektormezőket útfüggetlennek is. (Majd a később látjuk, hogy az "útfüggetlenséget" másképp is tudjuk definiálni.)

Tehát néhány igen fontos jelenséget, mint pl. a gravitáció vagy akár az elektrosztatikus erő, lehet modellezni vektormezőkkel. Kiderült, hogy ezeknek a "konzervatív" vektormezőknek igen különös tulajdonságaik vannak matematikai szempontból. A továbbiakban ezekről lesz szó.

***

Emlékezz, hogy a vektormező vonalintegrálja megadja a mező munkáját miközben egy test egy adott görbén végighalad. (Egyes esetekben a "mező munkájáról", máskor viszont a "mi általunk végzett" munkáról beszélünk, amit a mező ellenében végeztünk. Technikailag ezek közt nincs különbség, csak egy -1 szeres szorzó az eltérés)

A fent említett "útfüggetlenség" tehát azt vonja maga után, hogy az $$ \int_C \mathbf F \cdot d\mathbf s $$ vonalintegrál (azaz a munka) nem függ a C görbe alakjától, csak a görbe kezdőpontjától (legyen a), és a végponttól (b).

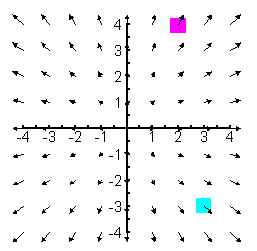
Vegyük példának az F(x,y) = (x,y) vektormezőt ami alul látható. Ez egy konzervatív (azaz "útfüggetlen") vektormező. A későbbiekben majd lesz róla szó, hogy hogyan tudjuk ezt bebizonyítani, most csak hidd el.
Szeretnénk kiszámolni az $$ \int_C \mathbf F \cdot d\mathbf s $$ vonalintegrált, ahol a kezdőpont a=(3,-3), a végpont pedig b=(2,4). Most a kezdőpontot a kék, a b-t pedig a magenta szinű négyzet jelöli.

Ahhoz, hogy demonstráljuk a konzervatív vektormezőket, alul három különböző görbe látható, kékkel, zölddel és pirossal. A görbék kezdő- és végpontja megegyezik. Minden görbén van egy pont amit mozgathatsz az animáción. Alul látható egy slider, amin a különböző vonalak az integrál értékét mutatják, az a-tól az aktuális pontig. Látható, ha minden pont a b-ben foglal helyet akkor a slideren megegyezik az értékük..
Míg rájössz hogyan kell mozgatni a pontokat az animáción, addig hadd mondjam el, hogy annak ellenére hogy a három görbén az integrál láthatóan megegyezik (vagyis ugyanannyi munkát végzünk, akármelyiken haladunk), ezzel még nem bizonyítottunk semmit. Ahhoz hogy bebizonyítsuk az útfüggetlenséget, végtelen sok görbén kéne elvégezni az integrált (bármely két pont között levő minden lehetséges görbén). Mit lehet ilyenkor tenni, hogyan bizonyítsuk be hogy a vektormező tényleg útfüggetlen? Majd később látni fogjuk, hogy ezt a problémát igen ötletesen oldották meg.

Java animáció megjelenítése / elrejtése (nem minden böngésző támogatja már)

Az animáción mellékesen az is látható, hogy görbéken végigmenve a vonalintegrálok a két végpont között nagyban változnak, csak akkor egyeznek meg amikor a b-ben (azaz magentában) vagyunk.

"Útfüggő" vektormezők

Ahogy fent is említettem, az "útfüggetlenség" a vektormezők csak egy speciális részére igaz.
Most a másik részükről is kell beszélnünk, ezek az ún. "útfüggő" vektormezők. Ezekről, a vonalintegrállal kapcsolatos példáknál már volt szó. Például az F(x,y) = (y,-x) egy tipikus nem-konzervatív vektormező (azaz "útfüggő").
Ebben az esetben ugye a munka amit végzünk függ a görbe alakjától amelyen a-ból b-be haladunk.

Na de miért van erről itt szó?
Alul látható, hogy ennek a mezőnek a vektorai az óramutató járásával megegyezően "cirkulálnak".
Kiderült, hogy ez a cirkuláció vagy "forgás" fogja megadni a kulcsot a fenti problémára (arra hogy végtelen sok görbét kellene megvizsgálni ahhoz, hogy eldöntsük konzervatív-e a vektormezőnk).
Észrevették, hogy az "útfüggő" vektormezők mindegyikében - kisebb vagy nagyobb mértékben - jelen van a cirkuláció, a konzervatív vektormezőkben viszont nincs! De a részletekről majd később..

A "cirkuláció" persze egy pontosan meghatározott dolog, és nem mindig a szó szerinti forgást jelenti. A képről nem mindig világos hogy van-e egy vektormezőnek cirkulációja. A cirkulációról már volt szó a vonalintegrál, mint cirkuláció részben.

Alul is látható, hogy a végzett munka most függ a görbétől. Kicsit más görbén haladva akár munkát sem kell végeznünk.
Pl. a kék görbét vizsgálva látjuk, hogy nincs munkavégzés, a másik kettőn viszont, ahogy az alsó "slidereken" is látszik, más-más munkát kell végeznünk. (A görbék ugye az alsó pontban kezdődnek, tehát "felfelé" haladnak.)

Java animáció megjelenítése / elrejtése (nem minden böngésző támogatja már)

A zöld görbe esetében a görbe iránya és a vektormező "iránya" többé-kevésbé megegyezik ezért azt várjuk hogy ott a vonalintegrál pozitív lesz:

$$ \int_C \mathbf F \cdot d\mathbf s > 0 $$

A piros görbe viszont éppen ellentétesen halad a vektormezővel, ezért:

$$ \int_D \mathbf F \cdot d\mathbf s < 0 $$ A kék görbénél pedig nincs munkavégzés: $$ \int_E \mathbf F \cdot d\mathbf s = 0 $$

Kapcsolódó:
A konzervatív vektormezőkben nincs cirkuláció
Az útfüggetlenség feltételeinek megértése - 1. rész
Potenciálfüggvény keresése