Stokes-tétel példák

Kapcsolódó cikkek:
Stokes-tétel
Felületi integrál
Rotáció

1. példa

Legyen C az alábbi zárt görbe:

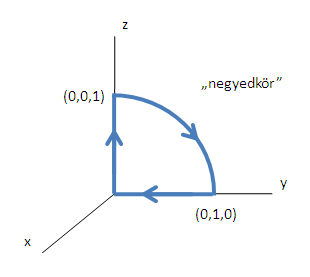
A vektormezőnk pedig legyen a következő: F(x,y,z) = (y, z, x).

A feladat, hogy a Stokes-tétel segítségével számoljuk ki a C menti vonalintegrált, az F vektormezőben.

Megoldás: A Stokes-tétel szerint a következőt kell kiszámolnunk:

$$ \iint_S \mbox{rot} \mathbf F \; \cdot d\mathbf S $$

, ahol \$S$\ egy felület amelynek harárvonala a fenti \$C$\ "negyedkörvonal". Azt, hogy konkrétan milyen \$S$\ felületet választunk mi dönthetjük el, a megkötés csak annyi, hogy a \$C$\ görbe legyen a felület határvonala.

Most elég egyértelmű, hogy a legegyszerűbb felület amit választhatunk az az \$yz$\-síkon levő negyedkör-felület.

Ezután a felületnek irányítást kell adnunk, azaz meg kell választanunk hogy melyik oldalán legyen a normálvektor. (ezzel azért kell foglalkozni, hogy "pozitív" végeredményt kapjunk, azaz ne kelljen előjelet cserélni a végeredménynél)
A görbe irányítása miatt, és a jobbkéz szabályt figyelembe véve melyik irányba kell, hogy mutasson a normálvektor ? (erről az előző cikk végén is írtam pár mondatot)
Látható hogy a jobbkéz szabály miatt a normálvektornak a negatív x-irányba kell mutatnia.

Továbbmenve, ezután ki kell számolnunk az \$\mathbf F$\ rotációját. A rotáció képlete a következő:

$$ rot \mathbf F = \left( \frac{\partial F_3}{\partial y} - \frac{\partial F_2}{\partial z}, \quad \frac{\partial F_1}{\partial z} - \frac{\partial F_3}{\partial x},\quad \frac{\partial F_2}{\partial x} - \frac{\partial F_1}{\partial y} \right) $$ ahol F₁, F₂, F₃ a komponensfüggvények.

(Megjegyzés: mivel ezt a formulát nem könnyű megjegyezni, ezért az idők során kialakult a rotációra egy egyszerűbben megjegyezhető "jelölés", ez pedig a következő: \$rot \mathbf F = \nabla \times \mathbf F$\ , ahol a \$ \nabla$\ ("nabla") szimbolikusan a következő vektort jelenti:

$$ \nabla = \left( \frac{\partial}{\partial x}, \frac{\partial}{\partial y},\frac{\partial}{\partial z} \right) $$

A vektoriális szorzat kiszámolására pedig viszonyag egyszerű emlékezni, csak egy 3x3-as determinánst kell kifejteni.

$$ rot \mathbf F = \nabla \times \mathbf F = \begin{vmatrix} \mathbf i & \mathbf j &\mathbf k \\ \frac{\partial }{\partial x} & \frac{\partial }{\partial y} & \frac{\partial }{\partial z}\\ F_1& F_2 & F_3 \end{vmatrix} $$ Megjegyzés vége)

Az \$\mathbf F = (y,\; z,\; x)$\ rotációja tehát így alakul:

$$ \begin{align} rot \mathbf F &= \nabla \times \mathbf F = \nabla \times (y,z,x)\\[7pt] &= \begin{vmatrix} \mathbf i & \mathbf j &\mathbf k \\ \frac{\partial }{\partial x} & \frac{\partial }{\partial y} & \frac{\partial }{\partial z}\\ y& z & x \end{vmatrix}\\[10pt] &=\mathbf i \left( \frac{\partial}{\partial y}x - \frac{\partial}{\partial z}z \right) - \mathbf j \left( \frac{\partial}{\partial x}x - \frac{\partial}{\partial z}y \right) + \mathbf k \left( \frac{\partial}{\partial x}z - \frac{\partial}{\partial y}y \right)\\[7pt] &= \mathbf i(-1) - \mathbf j(1) + \mathbf k(-1)\\ &= (-1,-1,-1) \end{align} $$

A következő lépés, hogy paraméteresen felírjuk a felületet (a negyedkört):

$$ \mathbf \Phi (r,\theta) = (0, \;r \cos \theta, r\;\sin \theta) \qquad 0\leq r \leq 1,\; \acute {es} \;\;0 \leq \theta \leq \pi /2 $$

A felületek paraméteres felírásáról (itt most \$r,\; \theta$\ voltak a "paraméterek") itt találhatsz egy rövid leírást.

Ezután pedig számoljuk ki a felület - egyik- normálvektorát (most nem kell, hogy egységnyi hosszú legyen):

$$ \begin{align} \frac{\partial \Phi}{\partial r} &= (0, \;\cos \theta,\; \sin\theta)\\ \frac{\partial \Phi}{\partial \theta} &= (0, \; -r \sin \theta, \;r\cos \theta)\\ \frac{\partial \mathbf \Phi}{\partial r} \times\frac{\partial \mathbf \Phi}{\partial \theta} &= \mathbf i(r \cos^2 \theta + r \sin^2 \theta) = r\mathbf i \end{align} $$

Látszik, hogy ez a normálvektor a pozitív-x irányba mutat, viszont nekünk nem ez kell hanem a negatív irányba mutató! Ezért a szorzatban megcseréljük az \$r$\ és \$\theta$\ változót:

$$ \frac{\partial \mathbf \Phi}{\partial \theta} \times\frac{\partial \mathbf \Phi}{\partial r} = -r \mathbf i $$

(Figyeld meg, hogy most a vektormező rotF= (-1, -1, -1) és a normálvektor n = (-r, 0, 0) többé-kevésbé egyirányba mutatnak, ami azt jelenti hogy a \$\displaystyle \iint_S rot \mathbf F \cdot d\mathbf S$\ felületi integrál várhatóan pozitív lesz.)

Ezekután pedig már minden megvan, hogy kiszámoljuk a tényleges felületi integrált, azaz megmondjuk a vonalintegrál értékét:

$$ \begin{align} \int_C \mathbf F \cdot d\mathbf s &= \iint_S \mbox{rot}\mathbf F \cdot \mathbf n \;dS\\[6pt] &=\int_0^1 \int_0^{\pi/2} \mbox{rot}\mathbf F(\Phi(r,\theta)) \cdot \left( \frac{\partial \Phi}{\partial \theta} \times \frac{\partial \Phi}{\partial r} \right) \;d\theta dr \\[6pt] &=\int_0^1 \int_0^{\pi/2} (-1, -1, -1) \cdot (-r,0,0)\; d\theta dr\\[6pt] &=\int_0^1 \int_0^{\pi/2} r \; d\theta dr = \frac{\pi}{4} \end{align} $$

2.példa, ellenőrzés

Most a fenti példát számoljuk ki a "hagyományos" módon, vagyis számoljuk ki közvetlenül a vonalintegrált. Ez jó lesz ellenőrzésnek, másrészt jobban lehet látni a Stokes-tétel és a hagyományos módszer közti különbségeket.

Ehhez fel kell írnunk paraméteresen a görbét. Ennek első lépése, hogy "feldaraboljuk" C₁, C₂, és C₃ részekre.

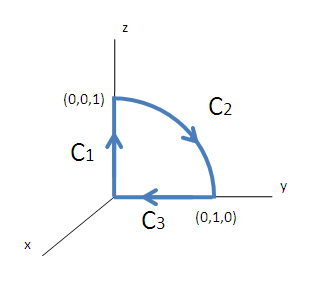A vonalinterált majd ezeken a részeken külön-külön kiszámoljuk és a kapott eredményeket összeadjuk: $$ \int_C \mathbf F \cdot d\mathbf s = \int_{C_1} \mathbf F \cdot d\mathbf s + \int_{C_2} \mathbf F \cdot d\mathbf s + \int_{C_3} \mathbf F \cdot d\mathbf s $$

A vektormező ugye F(x,y,z) = (y,z,x) volt.

Először \$C_1$\-en végezzük el az integrált. \$C_1$\-et paraméteresen felírva: $$ \mathbf c(t) = (0, \; 0,\;, t), \qquad 0 \leq t \leq 1 $$
Mivel \$\mathbf c'(t) = (0, 0, 1)$\ kiszámolhatjuk, hogy

$$ \begin{align} \mathbf F(\mathbf c(t)) \cdot \mathbf c'(t) &= \mathbf F(0,0,t) \cdot (0,0,1)\\[5pt] &=(0,t,0) \cdot (0,0,1)\\[5pt] &= 0 \end{align} $$

Így, $$ \int_{C_1} \mathbf F\cdot d\mathbf s = \int_0^1 \mathbf F(\mathbf c(t)) \cdot \mathbf c'(t) \;dt = 0 $$

Az integrál \$C_3$\ mentén ugyanúgy nulla lesz: $$ \int_{C_3} \mathbf F\cdot d\mathbf s = 0 $$

Végül pedig a \$C_2$\ mentén:
A \$C_2$\ görbét így paraméterezhetjük: $$ \mathbf c(t) = (0,\;\sin t\; \cos t) \qquad 0\leq t \leq \pi/2 $$

Mivel \$\mathbf c'(t) = (0, \;\cos t,\; -\sin t)$\, a vonalintegrál tehát ezen a görbén:

$$ \begin{align} \int_{C_2} \mathbf{F} \cdot d\mathbf{s} &= \int_{0}^{\pi/2} \mathbf{F}(\mathbf{c}(t)) \cdot \mathbf{c}'(t) \; dt \\ &= \int_{0}^{\pi/2} \mathbf{F}(0, \sin t, \cos t) \cdot (0, \cos t, -\sin t) \; dt \\ &= \int_{0}^{\pi/2} (\sin t, \cos t, 0) \cdot (0, \cos t, -\sin t) \; dt \\ &= \int_{0}^{\pi/2} \cos^2 t \; dt \\ &= \int_{0}^{\pi/2} \frac{1 + \cos 2t}{2} \; dt\\ &= \frac{t}{2} + \frac{\sin 2t}{4} \bigg|_0^{\pi/2} = \frac{\pi}{4} \end{align} $$

Ezért a teljes C-n a vonalintegrál:

$$ \int_{C} \mathbf{F} \cdot d\mathbf{s} = \frac{\pi}{4} $$

,ez pedig megegyezik azzal, amit az első példában a Stokes-tétellel kiszámoltunk.

3.példa

Van egy \$z^2 = x^2 + y^2$\ egyenlentű kúpunk, és ezt a kúpfelületet elmetsszük a \$z=1$\ síkkal. Így kaptunk egy görbét, a képen látható. (A görbe irányítása legyen az óramutató járásával ellentétes, a pozitív z-tengely felől nézve.)

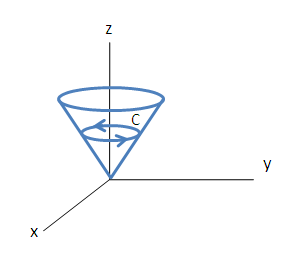A vektormező legyen: $$ \mathbf F(x,y,z) = \left( \sin x- \frac{y^3}{3},\;\cos y + \frac{x^3}{3},\; xyz\right) $$ Számoljuk ki a vonalintegrált a C görbére!

Megoldás: A Stokes tétellel számolva, az S felületre most két "természetes jelölt" is adódik.

Az egyik egy kisebb kúpfelület, a másik pedig egy körlap a \$z=1$\ síkon.
Én most a körlapot választom, (de ha ismered a kúpfelület paraméterezését, akkor azzal sem nehéz.)
Bármelyik felületet is válasszuk, most a normálvektornak "felfelé" kell mutatnia.

Folytatva, ezután ki kell számolnunk rotF-et, ami most $$ rot \mathbf F = (xz, \; -yz, \; x^2+ y^2) $$ lesz.

A fenti körfelületet a következőképp paraméterezhetjük: $$ \mathbf \Phi (r,\theta) = (r \cos \theta, r\;\sin \theta,\;1), \qquad 0\leq r \leq 1,\; \;\;0 \leq \theta \leq 2\pi $$

A egyik normálvektor most ez lesz:

$$ \frac{\partial \mathbf \Phi}{\partial r} \times\frac{\partial \mathbf \Phi}{\partial \theta} = (0, 0 ,r) $$ Látható, hogy ez a helyes irányba (felfelé) mutató normálvektor, tehát most ezt használjuk.

A felületi integrál pedig:

$$ \begin{align} \iint_S \mbox{rot} \mathbf F \cdot d\mathbf s &= \int_0^1 \int_0^{2\pi} \mbox{rot} (\mathbf F(r\cos \theta,\; r\sin \theta,\;1)) \cdot (0,0,r)d\theta dr\\[6pt] &= \int_0^1 \int_0^{2\pi} (r\cos \theta, -r\sin\theta, \;r^2)\cdot (0,0,r)d\theta dr\\[6pt] &= \int_0^1 \int_0^{2\pi} r^3 d\theta dr\\[6pt] &=\int_0^1 2\pi r^3 \; dr = \frac{\pi}{2} \end{align} $$